1 Introduction
Since their discovery by Hahn [1], echoes play a crucial role in the development of new experimental schemes in NMR. Solomon [2] extended the two-pulse sequence to the study of quadrupolar nuclei and observed multiple echoes for K127I (I = 5/2). More recently, there has been a renewal of interest for quadrupolar echoes (I = n/2, n ≥ 3) in static experiments, emphasizing (under precise assumptions) the location of echoes in the time domain and their nature [3–6]. Moreover, two experimental schemes designed for the total averaging of the second-order quadrupolar broadening are based on echoes: the Dynamic Angle Spinning (DAS) experiment [7], and the Multiple Quantum Magic Angle Spinning (MQ MAS) experiment [8]. In both cases, the echoes are obtained under macroscopic reorientation of the sample and are encoded by isotropic components. In that sense, both schemes lead to highly resolved spectra for quadrupolar nuclei.
In this paper, we present a pictorial representation of the various transitions (single quantum (SQ), or multiple quantum (MQ)) involved in the multilevel system of a given quadrupolar nucleus (I = n/2, n ≥ 3) (section 2). This approach is an extension of the ellipsoid representation [9] to higher orders of perturbation [10,11]. In section 4, we present a pictorial approach of the so-called Solomon echoes [2,5]: the location of the echoes as well as their nature (SQ and/or MQ – allowed or forbidden) will be derived very easily. The experimental evidence of Solomon echoes for an aluminophosphate cluster (27Al, I = 5/2) [12] will be presented subsequently. In section 4, the DAS and MQ MAS experiments will be illustrated by averaged surfaces. The equations of these averaged surfaces can be derived analytically under fast rotation. The main results concerning DAS and MQ MAS (isotropic shifts...) will be easily derived. We note that our approach is essentially Cartesian and that explicit reference to the Legendre polynomials is not necessary. Moreover, we believe that such a representation may unify the notion of echo in both static and rotating modes.
2 Pictorial representation of transitions for a quadrupolar nucleus I = n/2 (n ≥ 3)
Following Man [13,14], we define the line shift in Σobs (see below) related to the transition between two energy levels |m′〉 and |m〉 by:
| (1) |
Σobs corresponds to the frame rotating with the angular frequency ω0 relative to the laboratory frame Σlab. In Eq. (1), HQ(1) and HQ(2) correspond to the first-order and the second-order term of the quadrupolar Hamiltonian in standard perturbation theory, respectively [15]. When m′ = m – 1, the SQ transitions are described. m = 1/2 corresponds to the central transition (CT), which is not shifted by the first-order quadrupolar interaction. m ≠ 1/2 corresponds to the (2I - 1) satellite transitions (ST). When m′ ≠ m – 1, the MQ transitions are described. Assuming ηQ = 0 for simplicity, the terms ωm′,m(1)static and ωm′,m(2) static in Eq. (1) are given by [11]:
| (2) |
| (3) |
β0 corresponds to the polar angle of B0 in the quadrupolar PAS (principal-axis system). In order to introduce our pictorial representation of transitions, we focus first on the first-order term, ωm′,m(1)static. Consider the quadric (second-degree surface), whose equation in the quadrupolar PAS is given by [10]:
| (4) |
Assuming m2 > m′2, this surface corresponds to a hyperboloid of one sheet. The intersection of the surface with the B0 direction leads to the intersection radius r given by: r–2 = (m2 – m′2) (1 – 3 cos2β0). It follows that (+r–2) is directly related to the angular part of the first-order shift (Eq. (2)). For β0 < ξm = 54.74° (the magic angle), the intersection radius cannot be defined. We use then the complementary quadric, given in the PAS by:
| (5) |
It corresponds to a hyperboloid of two sheets. The intersection of the complementary surface with the B0 direction leads to the intersection radius r given by: r–2 = (m2 – m′2) (3 cos2β0 – 1). (–r–2) is related to the angular part of Eq. (2).
It follows that the first-order shift, ωm′,m(1)static, corresponding to the transition between |m′〉 and |m〉, can be safely illustrated by a set of two complementary hyperboloids. Each surface is ‘signed’ (+ or –), as (+r–2) or (–r–2) leads alternatively to the angular part of Eq. (2). This representation can be generalized to ηQ ≠ 0: two complementary elliptic hyperboloids are then necessary (when ηQ = 0, the corresponding surfaces are of revolution – see above). Considering the second-order shift, ωm′,m(2)static, we have shown previously that quadrics cannot be connected to the angular part of Eq. (3) [11]. However, a set of signed complementary homogeneous quartics (fourth-degree surfaces) can achieve this goal. As an example, we consider the central transition (m′ = m – 1, m = 1/2), which is subjected solely to second-order effects. Eq. (3) leads to:
| (6) |
We define two complementary quartics in the quadrupolar PAS by:
| (7) |
The radius r corresponding to the intersection of the surfaces with the B0 direction are given by: (±r–4) = (3/8) sin2β0 (9 cos2β0 – 1). It corresponds exactly to the angular part of Eq. (6). At this point, several comments can be made:
- • (i) when ηQ ≠ 0, generalised quartics can always be defined; explicit Cartesian equations of these surfaces are given in [11];
- • (ii) considering both terms, ωm′,m(1)static and ωm′,m(2)static (Eqs. (2) and (3)), the involved angular part Ang{ωm′ ,mstatic} can always be illustrated by a set of complementary quartics; it follows then that (±r− 4)=Ang{ωm′ ,mstatic};
- • (iii) for any higher order of perturbation (n), homogeneous surfaces of degree 2n are able to illustrate the shifts, assuming (±r− 2n)=Ang{ωm′ ,mstatic}; for instance, sixth-degree surfaces [16] are directly connected to third-order effects on quadrupolar transitions [17].
The pictorial representations of all SQ and MQ transitions for a spin I = 3/2 are presented in Fig. 1.
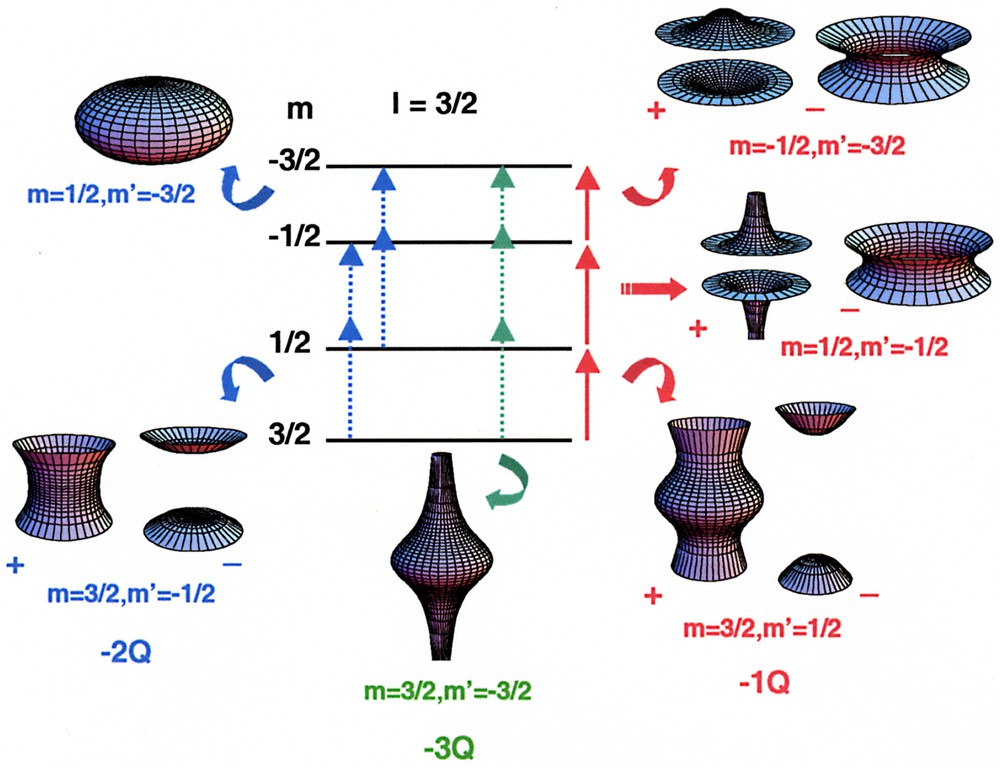
Pictorial representation of SQ and MQ transitions for a quadrupolar I = 3/2 nucleus. The signed quartics verify: (±r− 4)=Ang{ωm′,mstatic} (Eqs. (2) and (3)) – the ratio of the constants in Eqs. (2) and (3) is arbitrary fixed. For the CT (m = 1/2, m' = –1/2) and the –3Q transition (m = 3/2, m' = –3/2), only second-order effects are represented (as ωm′,m(1)static vanishes in both cases (Eq. (2)).
3 Pictorial approach of Solomon echoes [2,5]
3.1 Description of evolution and refocusing of coherences by hyperboloids
The main purpose of this section is to illustrate very easily the time-domain response of a quadrupolar nucleus, subjected to a two-pulse sequence (see Fig. 2). Only the first-order quadrupolar interaction is considered, and dipolar couplings with other nuclei are neglected (these assumptions correspond to the quadrupolar Solomon echoes, in contrast with the so-called quadrupolar Hahn echoes [4,5,14]). The location of the various echoes in the τ4 domain (Fig. 2), as well as their nature (SQ and/or MQ), is obtained by using the surfaces defined by Eqs. (4) and (5). As the SQ observable transitions are considered in the τ4 period, we focus first on the ST: each ST (m′ = m – 1) is characterised by two signed complementary hyperboloids (Eqs. (4) and (5)). For a given orientation β0 of B0 in the quadrupolar PAS (assuming ηQ = 0 for the sake of simplicity), the shift of a particular crystallite is given by the signed intersection radius (see above). It follows that a given ST can refocus any transition (either SQ or MQ) characterised by a set of hyperboloids of opposite signs! We note that the CT cannot refocus evolutions occurring during τ2, as hyperboloids cannot be defined for this particular transition (m2 = m′2).
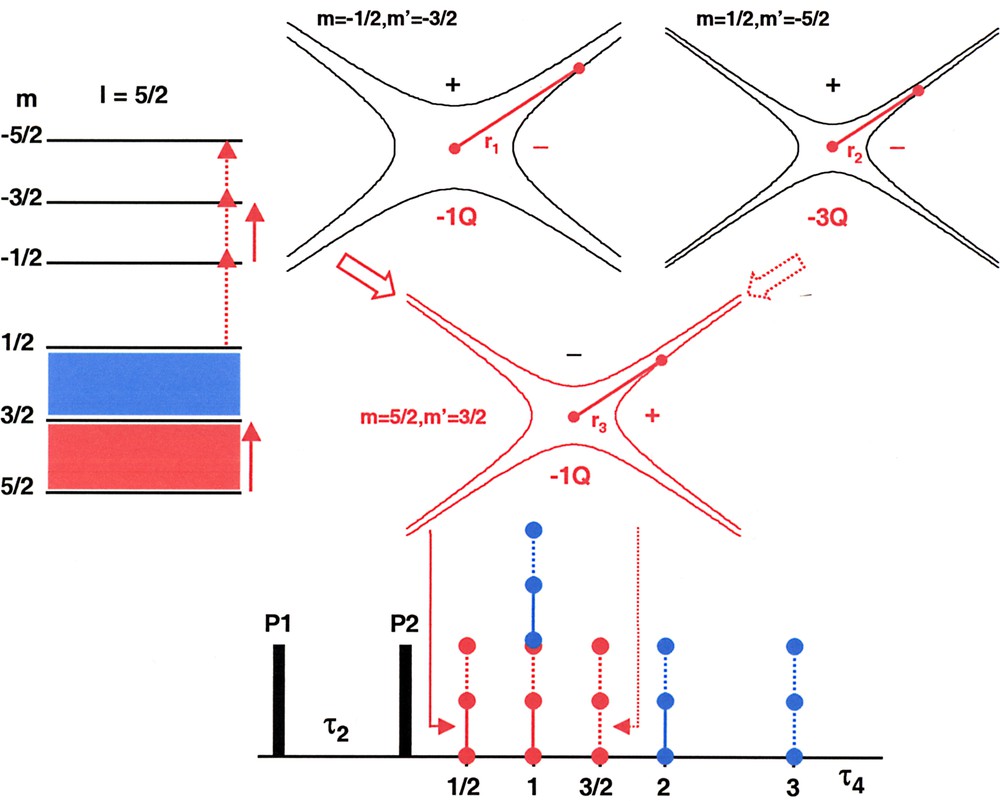
Solomon echoes following a two-pulse sequence (P1, P2) (I = 5/2). τ4 is given in τ2 units. In red: refocusing of coherences by the (3,5–1Q) SQ ST. In blue: refocusing of coherences by the (1,3–1Q) SQ ST. Vertical solid line: refocusing of two ±1Q coherences. Vertical dashed-line: refocusing of two ±nQ coherences. Signed hyperboloids in red: corresponding to the (3,5–1Q) SQ ST. Signed hyperboloids in black: corresponding to the (–3,–1–1Q) SQ transition and to the (–5,1–3Q) MQ transition. The contributions refocused by the (–3,–1–1Q) SQ ST and the (–5,–3–1Q) SQ ST are omitted for clarity.
Let us take an example: we consider the (3,5–1Q) SQ ST (m = 5/2, m′ = m–1 = 3/2, or m2 – m′2 = 4) for an I = 5/2 nucleus. The corresponding signed hyperboloids are shown in Fig. 2. Obviously, this SQ transition can refocus the τ2 evolution governed by the (–3,–1–1Q) transition (m1 = –1/2, m′1 = –3/2), as this transition is represented by a set of hyperboloids of opposite signs. The echo occurs at . Considering the (–5,1–3Q) transition (m2 = 1/2, m'2 = –5/2), the refocusing by the (3,5–1Q) ST leads to an echo located at . Our approach leads therefore to the exhaustive description of the contributions refocused by the (3,5–1Q) ST: (3,11Q), (3,–12Q), (–3,–1–1Q), (–3,1–2Q): echo at τ4 = 1/2 τ2; (5,31Q), (5,–34Q), (–5,–3–1Q), (–5,3–4Q): echo at τ4 = τ2; (5,12Q), (5,–13Q), (–5,–1–2Q), (–5,1–3Q): echo at τ4 = 3/2 τ2. Several comments can be made:
- • (i) using the same procedure, echoes located at τ4 = τ2, 2 τ2, 3 τ2 are predicted for the contributions refocused by the (1,3–1Q) SQ ST (m = 3/2, m' = m – 1 = 1/2) (Fig. 2); the contributions refocused by the (–3,–1–1Q) and (–5,–3–1Q) SQ ST lead to echoes located at the same time in the τ4 domain;
- • (ii) the nature of each echo (allowed or forbidden) is easily determined by our approach; the τ4 = 3/2 τ2 and 3 τ2 echoes are called ‘forbidden’ echoes, as they correspond to the refocusing of MQ coherences exclusively; the τ4 = 1/2 τ2, τ2 and 2 τ2 are called ‘allowed’ echoes; we note in particular that the τ4 = 2τ2 allowed echo corresponds to the refocusing of ±1Q and ±4Q coherences (see below);
- • (iii) antiechoes, as well as transients [3,6] can also be described by the surfaces presented above; they are not represented in Fig. 2;
- • (iv) the representation of transitions by surfaces is particularly useful for the location and description of multiple echoes involved in 3- (or more) pulse sequences [3];
- • (v) when second-order quadrupolar effects and/or dipolar interactions are present [6], the location and nature of echoes can be adequately described by using quartics (see above) and/or hyperboloids.
3.2 Experimental evidence of Solomon echoes: 27Al (I = 5/2)
Solomon echoes were observed very rarely. Echoes in K81Br (I = 3/2) were reported by Bonera et al. [18] and in 23NaN3 (I = 3/2) by Jeffrey [19]. We note that for I = 3/2 one single echo at τ4 = τ2 is observed. Multiple echoes were observed by: (i) Solomon [2] in the case of K127I (I = 5/2), (ii) Sanctuary and Halstead [3] using K127I and two- or three pulse sequences, (iii) Schoep et al. [20] in a series of 51V3X compounds (I = 7/2). To the best of our knowledge, multiple echoes in the frame of 27Al solid-state NMR were never reported in the literature and only mentioned once by the authors [12].
In Fig. 3a, the structure of a cubane-shaped Al–O–P cluster is presented. The synthesis and characterisation by solid-state NMR of this cluster is presented in [12] (δiso(27Al) = –8.7 ppm; CQ = 1.70 MHz; ηQ = 0.3; δiso(31P) = –25.7 ppm; δ11 = –61.0, δ22 = –31.9, and δ33 = 15.7 ppm). Using a two-pulse sequence, multiple echoes located at τ4 = τ2/2, τ2, and 2 τ2 are clearly observed (Fig. 3b). They correspond to ‘allowed’ echoes. The observed echoes are superimposed to a residual FID component. Using the general concept of phase cycling [21], it is possible to select only 2Q coherences through the echo sequence. The time-domain response for the Al–O–P cubane is presented in Fig. 3c. Obviously, the FID component is remarkably suppressed, leading to an improved observation of the echoes. In this case, the τ4 = 3/2 τ2 and 3 τ2 ‘forbidden’ echoes are observed. Moreover, we note that the τ4 = 2 τ2 echo is not observed. Indeed, it corresponds to the refocusing of ±1Q and ±4Q coherences (see above), which are rejected by the 2Q filter.
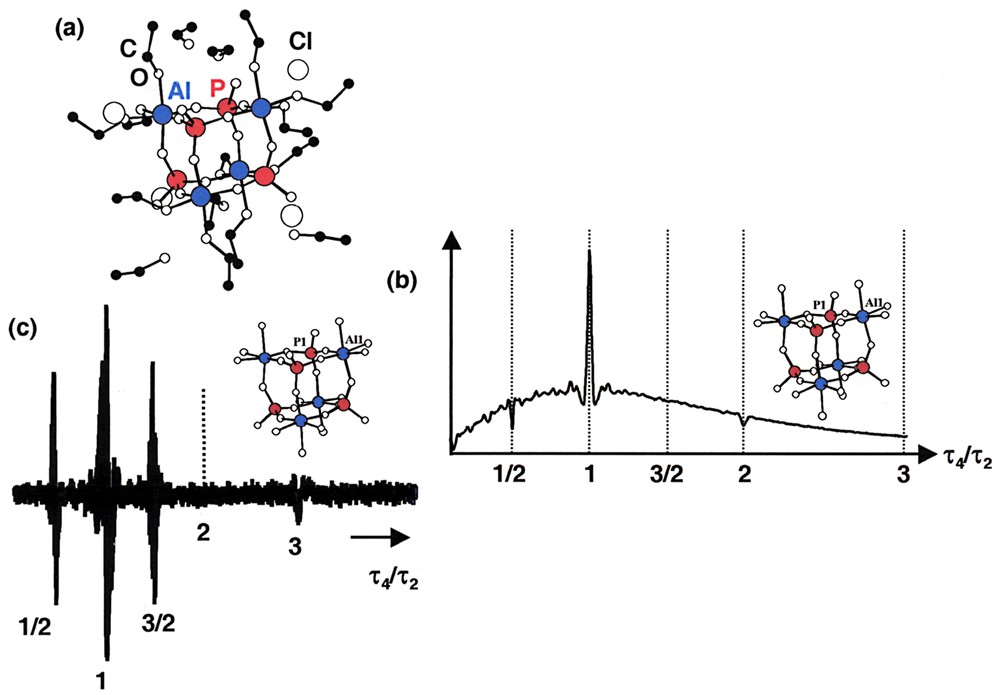
(a) Al–O–P cubane-shaped cluster [12]. One Al1 and one P1 crystallographic sites. Al and P atoms are linked by oxo bridges. Cl– are present as counter-anions. Al atoms are 6-fold coordinated (including three ethanol molecules as ligands). Four solvate ethanol molecules per cubane entity are present. (b) Solomon-‘allowed’ echoes located at τ4 = 1/2, 1 and 2 τ2. These echoes are superimposed on a FID. (c) Selection of 2Q coherences through phase cycling: P1, +X +Y –X –Y; P2, +X +X +X +X; Rec: +X –X +X –X. ‘Allowed’ and ‘forbidden’ echoes are observed. The FID is suppressed. The τ4 = 2 τ2 echo is missing.
We believe that the quantitative study of the echo amplitudes could be an interesting alternative for the structural characterisation of compounds for which the CQ quadrupolar constants are fairly small.
4 Pictorial approach of DAS [7,22] and MQ MAS [8]
In this section, the surfaces described above (mainly quartics) will be used for the pictorial representation of macroscopic reorientations of samples in the case of DAS and MQ MAS experiments. Both schemes are 2D experiments, including a highly resolved dimension. Moreover, DAS and MQ MAS, are based on echoes under rotation, encoded with isotropic components. The ‘static’ quartics defined by Eqs. (3), (6), and (7) are sufficient for a quantitative description of the DAS and MQ MAS experiments! The key concept is to consider averaged surfaces, mimicking the fast reorientation of the sample: the ‘static’ equation is first written in a rotor frame (XRYRZR), which is oriented by the Euler angles (α,β,γ) from the quadrupolar PAS [11]. Spinning the sample implies that γ becomes time-dependent. Under rapid rotation and after averaging, the quartics related to the CT (Eq. (7)) are given by (assuming ηQ = 0 for the sake of simplicity):
| (8) |
| (9) |
The shift under fast rotation at θ1° (macroscopic angle) is then simply given by (±rβ– 4)θ1° (rβ corresponds to the intersection radius of the averaged quartics with the B0 direction). It is well known that fast reorientation around a single axis is not sufficient for the total removal of quadrupolar second-order effects. The DAS experiment can be viewed as an evolution at θ1° followed by an evolution at θ2° during k. If high resolution is attained, the following equation must be fulfilled:
| (10) |
Equation (10) is the direct geometrical representation of the DAS scheme. Using Eq. (9), Eq. (10) can be analytically solved, leading to the well-known DAS angle pairs [11,23]:
The MQ MAS experiment can be illustrated as well. We consider first the ‘static’ surface corresponding to ω−3/2,3/2(2)static (–3Q coherence), defined by Eq. (3) (I = 3/2). The corresponding set of quartics is given by (assuming ηQ = 0 for the sake of simplicity) [11]:
| (11) |
(see Fig. 1). Under fast rotation, the averaged surfaces are given by:
| (12) |
| (13) |
Spinning around a single axis (at θ°), the evolution under the MQ coherence followed by the evolution under the CT (during k) can be described geometrically by:
| (14) |
Again, high-resolution is attained if C2 is a constant, independent of β. Eq. (14) is fulfilled if θ° = θm = 54.74° and k = 7/9; this is the MQ MAS experiment for a I = 3/2 nucleus. This approach can be extended to every value of I and every order of coherence [11].
We note the complete analogy between the DAS and the MQ MAS experiments (see Eqs. (10) and (14)). In the DAS experiment, a single averaged surface (CT) is involved and two intersection radii at θ1° and θ2° are necessary for the pictorial representation of the DAS echo. In the MQ MAS experiment, two averaged surfaces (CT and MQ) are involved and a single intersection radius at θ° = θm is necessary for the pictorial representation of the MQ MAS echo. These results are illustrated in Fig. 4.
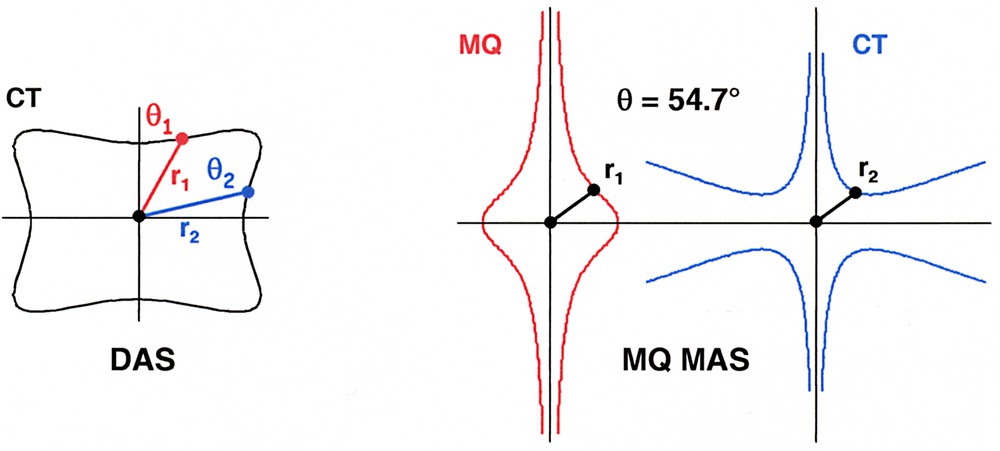
Pictorial representation of DAS: the averaged CT surface is intersected at two different angles. r1 and r2 verify Eq. (10). Pictorial representation of MQ MAS: both averaged surfaces (CT and –3Q, I = 3/2) are intersected at one unique angle (the magic angle). r1 and r2 verify Eq. (14).
5 Conclusion
We have shown that the various transitions involved in the multilevel system of a quadrupolar nucleus (I = n/2, n ≥ 3) can be safely illustrated by quadrics and quartics. Using quartics, it is possible to take second-order effects in account. The only prerequisite is the knowledge of the energy levels, corrected by standard second-order perturbation theory. The interpretation of Solomon multiple echoes becomes then very simple, by using sets of complementary hyperboloids. This approach becomes very efficient when more than two pulses are involved in the pulse sequence. We have also shown that the quadrupolar echoes under fast rotation of the sample can be as well illustrated by using averaged quartics. The number and nature of the used quartics depend mainly on the chosen experimental scheme (DAS or MQ MAS).
Acknowledgements
Dr. P. P. Man is warmly acknowledged for helpful discussions concerning the quadrupolar echoes.


