1 Introduction
It is impossible to underestimate the influence of Alfred Werner upon the development of coordination chemistry [1] yet paradoxically it was Werner’s recognition of the invariability of coordination number 6 for Cr(III) and Co(III) complexes in particular, and for transition metals in general, that may have delayed for years the recognition of the ability of the lanthanides to achieve high coordination numbers in their complexes. Assignment of precise coordination numbers to the central atom in complexes of Cr(III) and Co(III) (not to mention Pt(II) and C(IV))), was facilitated by their kinetic inertness, this enabling the isolation of isomers for example. Understanding the ability of the lanthanides to exhibit high coordination numbers was not achieved until relatively fast X-ray diffraction methods could be brought to bear on the problem. A further factor complicating the issue was the uncertainty of coordination, not only by water and other solvent molecules, but also other ligands like nitrate, 1,10-phenanthroline and crown ethers, all of which exhibit variable ligation characteristics. Add to that the weakness of UV/visible spectra lines and their frequent insensitivity to coordination geometry, and the independence of magnetic behaviour of coordination number, and it is scarcely surprising that the coordination chemistry of the lanthanides took much longer to develop than that of the transition metals [2–11].
X-ray diffraction was used to establish coordination number 9 (and tricapped trigonal prismatic coordination – it should be parenthetically remarked that regular polyhedra in lanthanide complexes are associated with an array of identical ligands) for the neodymium ion in [Nd(H2O)9] (BrO3)3 in 1939 [12], yet it was still possible as late as 1963 for a chemist of the eminence of H.J. Emeleus to insist that yttrium and the lanthanides would be six-coordinate in their complexes [13] (Fig. 1).
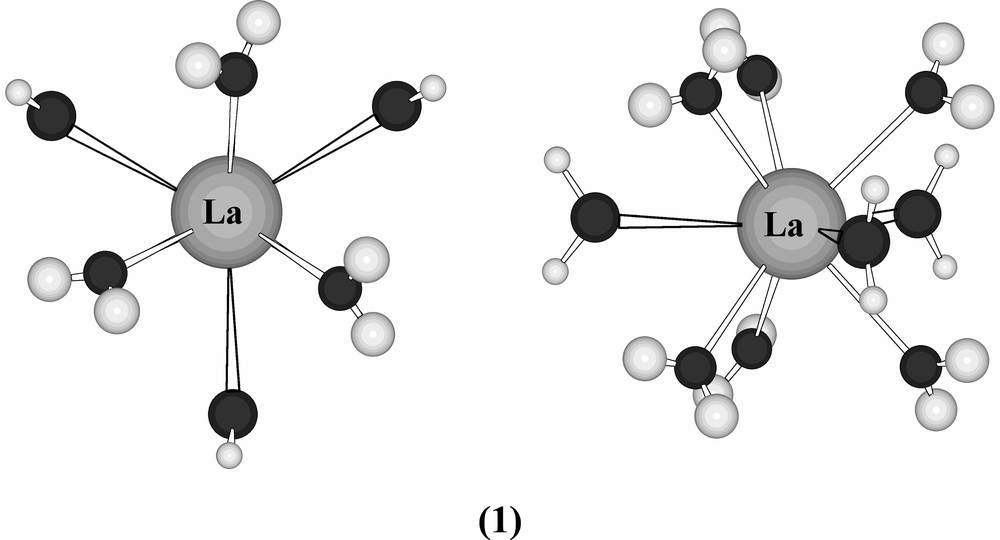
The [La(H2O)9]3+ ion (1) viewed (left) along and (right) perpendicular to the threefold axis of the cation.
2 Factors affecting coordination numbers in lanthanide complexes
In contrast to transition-metal complexes, where the coordination number for a particular combination of metal ion and oxidation state is often constrained to a particular value, the coordination number in lanthanide complexes appears to be substantially determined by crowding in the coordination sphere, whilst bearing in mind the strength of the positively-charged metal ion and the electron-rich ligand. At all events, high coordination numbers are predicted for the lanthanides simply upon the basis of the large size of the lanthanide ions.
It is necessary to distinguish between first-order and second-order steric effects [14].
The term first-order crowding refers to congestion among the donor atoms bound directly to the lanthanide ion; a situation in which inter-donor atom repulsions make it impossible for more atoms to be packed in ‘direct contact’ with the lanthanide. Examples of such donors are halide or oxide ions; water, hydroxide or thiocyanate. These lead to compounds with normal or ‘high’ coordination numbers.
The term second-order crowding refers to situations where the groups attached to the donor atoms exhibit considerable ‘presence’, and it is interactions between these groups that determine how many of the ligands can bind to the lanthanide, rather than inter-donor repulsions. Examples of these donors are –N(SiMe3)2, –CH(SiMe3)2, –C(SiMe3)3, bulky alkoxides and aryloxides. These lead to compounds with very low coordination numbers.
2.1 Establishing high coordination numbers
It was only with the increasing use of X-ray diffraction techniques that the breakthrough was achieved in 1965 with the determination of the structure of K [La(edta)(OH2)3]·5 H2O [15] (9-coordinate) and [La(Hedta)(OH2)4] [16] (10-coordinate).
The structure of [Eu(terpy)3] (ClO4)3 (terpy = 2, 2′: 6′, 2′′-terpyridine) showed [17] that three terpyridyl ligands might fit around a lanthanide ion, affording a coordination number of 9 whilst [La(bipy)2(NO3)3] (2) was found to be 10-coordinate with bidentate nitrate groups [18] (Fig. 2).
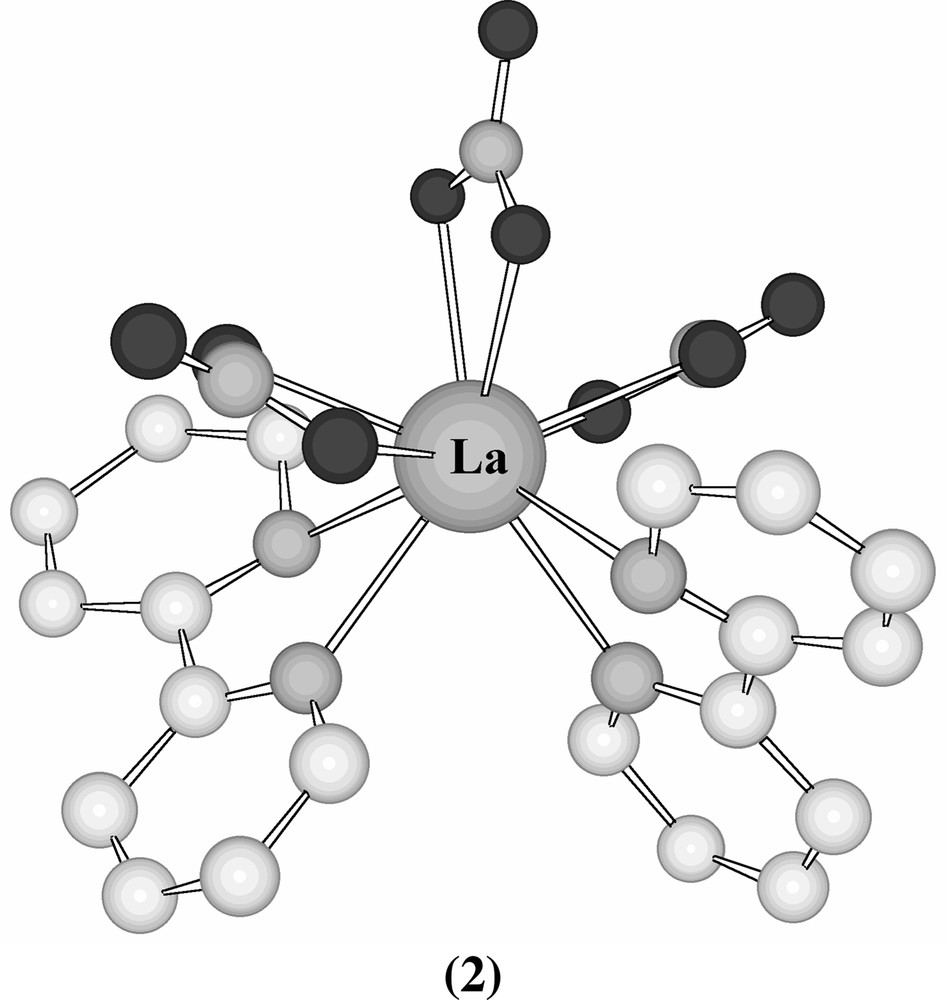
Structure of [La(bipy)2(NO3)3] (2).
Around this time, it was also realized that the β-diketonate complexes [Ln(diketonate)3], although formally similar to established octahedral complexes formed by the transition metals, such as [Fe(acac)3], were often obtained with added solvent molecules; diffraction studies showed a coordination number of 8 in [La(acac)3 (H2O)2] [19] and this tendency of [Ln(diketonate)3] to bind Lewis bases was subsequently utilised in the area of NMR shift reagents [20–22].
These and other structures established the concept of CN > 6 as the norm. It has subsequently been shown that coordination numbers up to 12 are attainable using ligands with small ‘bite angle’ such as nitrate and 1,8-naphthyridine (naph), in [Pr(naph)6] (ClO4)3 [23] and salts of the [Ln(NO3)6]3– ion (Ln = La, Ce, Pr, Nd) [24].
2.2 Establishing low coordination numbers
By the early 1970s, the focus now shifted to the question of whether coordination numbers below 6 could be achieved. In 1969, it had been shown that the three-coordinate complex [Fe(N(SiMe3)2)3] could be obtained by use of a bulky silylamide ligand (the Ti, V and Cr analogues were soon also prepared, as subsequently were the Mn and Co analogues). A natural extension of this work led to the synthesis of [Ln(N(SiMe3)2)3] (Ln = La–Lu except Pm; Y) [25], shown by diffraction methods to be the first three-coordinate lanthanide compounds [26–28]. Unlike the transition-metal analogues, that have strictly planar MN3 cores, the MN3 moiety is pyramidal (3) in the lanthanide compounds (Fig. 3, see Section 6).
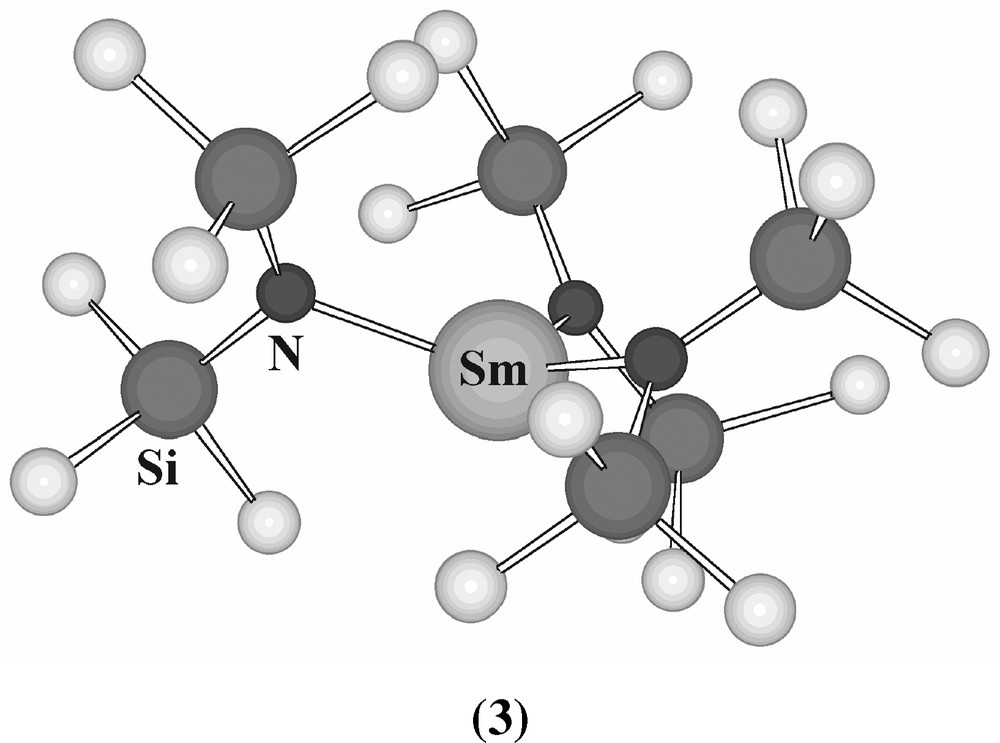
Structure of [Sm(N(SiMe3)2)3] (3).
These compounds were subsequently shown to form four-coordinate Ph3PO adducts such as [{La{N(SiMe3)2)3}(Ph3PO)] [29] and indeed five-coordinate bis(nitrile) adducts [Ln(N(SiMe3)2)3(CyNC)2] (Ln = Y, La–Nd, Sm, Eu, Tb–Ho, Tm-Yb; Cy = cyclohexyl) with axial nitriles have more recently been reported [30].
Another approach to low coordination numbers involved the use of bulky aryls, the first four-coordinate lanthanide compounds to be characterized being [Li(THF)4]+ [Lu(2,6-Me2C6H3)4]– (4) and the Yb analogue [31] (Fig. 4).
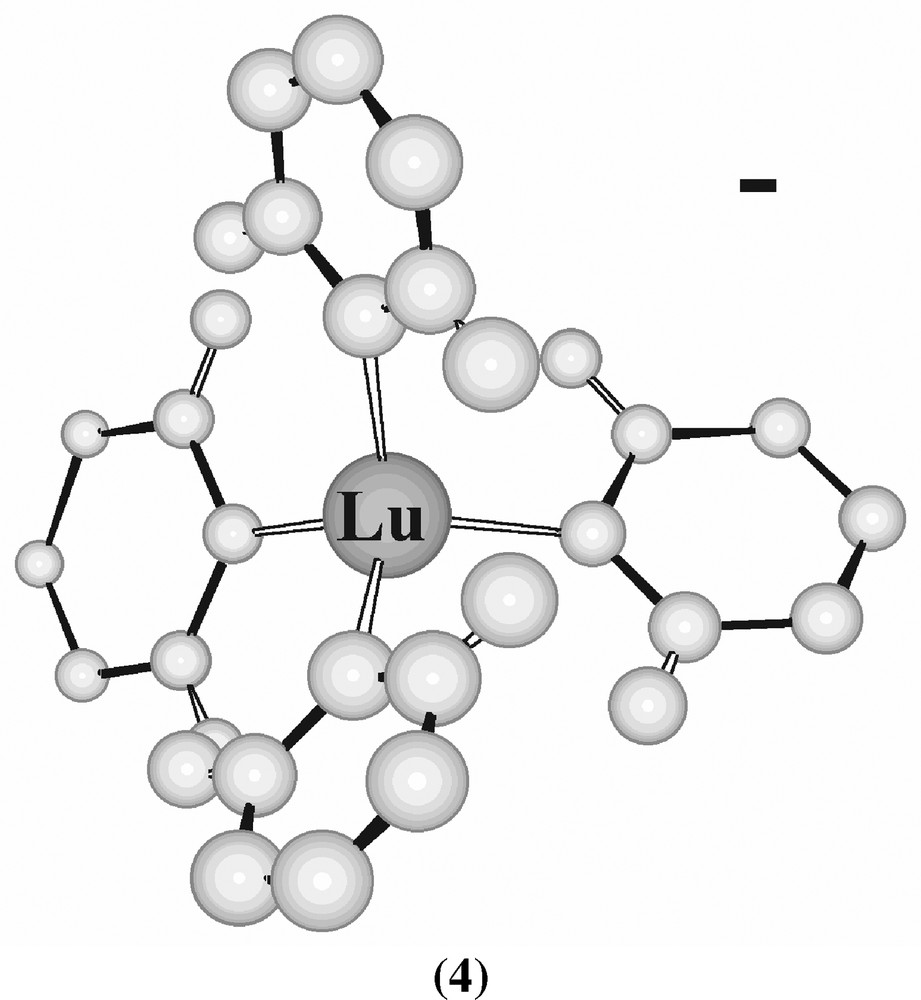
Structure of [Lu(2,6-Me2C6H3)4]– (4).
More recently, three-coordinate alkyls have been synthesised, the first being [Ln{CH(SiMe3)2)3] (Ln = La, Sm) [32], followed by others (Ln = Y, Pr, Nd, Er and Lu [33]). They have pyramidal structures, similar to those found in the silylamides [Ln{N(SiMe3)2}3], with La–C 2.515(9) Å and Sm–C 2.33(2) Å. These were synthesised starting from [Ln(OC6H3But2-2,6)3], thus obviating the possibility of chloride retention.
Use of a bulky silicon-substituted t-butyl ligand has even permitted the isolation [34,35] of simple two-coordinate monomeric (bent) alkyls [Ln{C(SiMe3)3}2] (Ln = Eu, Yb) which are sublimeable in vacuo.
2.3 Low coordination numbers that are not always all that they seem – alkoxides and aryloxides
In the case of alkoxides and aryloxides, it is harder to get monomers with low coordination numbers, since –OR ligands by their own nature exert less second-order influence in the coordination sphere than the corresponding –NR2, and, for the same reason, –OR groups are much more likely to be found in bridging positions. Thus, because of oligomerisation and/or the presence of solvent in the coordination sphere, Ln(OR)3 species are frequently not three-coordinate. Thus ‘Nd(OCHPri2)3’ is a binuclear solvate, [Nd(OCHPri2)3(thf)]2, having the five-coordinate structure [(Pri2CHO)2(thf)Nd(μ-OCHPri2)2Nd(thf)(OCHPri2)2] [36]. Similarly, the neopentoxides Ln(OCH2But)3 (Ln = La, Nd) are tetrameric [Ln(OCH2But)3]4 based on a square of lanthanides with each lanthanide bound to one terminal and four bridging alkoxides; moreover, IR spectra in both the solid-state and solution show bands ascribed to Ln···H–C agostic interactions (a factor increasing coordination numbers that could not have been deduced without the availability of fast crystal structure determination) so this structure appears to persist into solution [37]. ‘Gd{OSi(SiMe3)3’ is [Gd{OSi(SiMe3)3}3(thf)2], with a trigonal bipyramidal structure [38]. [La(OCPh3)3]2 and [Ce(OSiPh3)3]2, are [La(OCPh3)2(μ-OCPh3)]2 and [Ce(OSiPh3)2(μ-OSiPh3)]2 respectively, both with four-coordinate lanthanides [39].
Using an even bulkier ligand [40] affords the compound Ce(OCBut3)3, which is believed to be a monomer; it undergoes high-yield thermolysis in vacuo at 150 °C, affording an alkoxy-bridged dimer [(But2CHO)2Ce(μ-OCHBut2)2Ce(OCHBut2)2] with four-coordinate cerium:
2 Ce(OCBut3)3 → [Ce(OCHBut2)3]2 + 6 C4H8
Aryloxides are more fertile in affording low-coordinate monomers, through the use of bulky substituents in the 2,6 positions of the benzene ring. With the relatively unhindered 2,6-dimethylphenoxide ligand, Y(OC6H3Me2-2,6)3 is isolated as six-coordinate [Y(OC6H3Me2-2,6)3(thf)3] and five-coordinate [Y(OC6H3Me2-2,6)3(thf)]2 [41]. Terbium gives two monomers, fac-[Tb(OC6H3Me2-2,6)3(thf)3] and [Tb(OC6H3Pri2-2,6)3(thf)2] [42].
The slightly bulkier 2,6-diisopropylphenolate ligand leads to unsolvated Ln(OC6H3Pri2-2,6)3 species, which are in fact η6-arene bridged dimers Ln2(OC6H3Pri2-2,6)6; in thf, they form conventional trigonal bipyramidal thf adducts [Ln(OC6H3Pri2-2,6)3(thf)2] (Ln = Pr, Nd, Sm, Gd, Er, Yb, Lu) [43]. [La2(OC6H3Pri2-2,6)6] reacts with CsOC6H3Pri2-2,6 and affords [CsLa(OC6H3Pri2-2,6)4]. The latter contains alternating Cs+ and [La(OC6H3Pri2-2,6)4]– ions in a one-dimensional chain structure held together by Cs-arene polyhapto-interactions [44]. The precise nature of these interactions is not wholly understood; certainly the use of the term ‘π’ should not be taken as implying a covalent contribution to the bonding comparable with transition metal complexes.
The 2,6-diphenylphenolates [Ln(OC6H3Ph2-2,6)3] (Ln = La, Ce, Pr, Nd, Gd, Ho, Er, Lu, Y) have monomeric structures with the lanthanide slightly out of the O3 plane, but with some additional ring–metal interactions [45]. [Ln(OC6H3Ph2-2,6)3(thf)2]·2 thf (dpp = 2,6-diphenylphenolate; Ln = La, Nd) have ‘conventional’ five-coordinate trigonal bipyramidal coordination of the metal with one axial and one equatorial thf [46]; in contrast, [Nd(OC6H3Ph2-2,6)3(thf)] has pseudo-tbp coordination with three equatorial phenoxides, an apical thf and an apical position occupied by a phenyl group; as already noted, unsolvated [Nd(OC6H3Ph2-2,6)3] also features Nd-ring polyhapto interactions.
Four-coordinate anionic diphenylphenolates [Na(diglyme)2][Ln(OC6H3Ph2-2,6)4] and [Na(dme)3][Ln(OC6H3Ph2-2,6)4] have been made [47], whilst ‘unsolvated’ [NaLa(OC6H3Ph2-2,6)4] contains [La(OC6H3Ph2-2,6)4]– with sodium bound to three oxygens and interacting with three different phenyl groups [45]. Using 2,6-di-tert-butylaryloxides, three-coordinate species can be obtained, such as [48] [Ln(OC6H3But2-2,6-Me-4)3] (Ln = Y, La, Pr, Nd, Dy–Er, Yb) and [Ln(OC6H3But2-2,6)3] (Ln = Y, La, Sm). In these three-coordinate species, the possibility arises of the LnO3 grouping being planar or pyramidal; both possibilities seem to be realised. [Y(OC6H3But2-2,6)3] is trigonal planar [49] but [Ce(OC6H2But2-2,6-Me-4)3] is pyramidal [50]. Possibly the balance of small and variable ‘agostic’ and Van der Waals forces, whether within the lattice or within the complex species, is the determining factor. [Ln(OC6H3But2-2,6)3] (Ln = Pr, Nd) are also three-coordinate [51].
3 The aqua ions
The nature of the lanthanide aqua ion has been the source of much study but now appears to be fairly well understood. Much of the evidence (though not the most recent) has been thoroughly reviewed [52]. An early influential piece of spectroscopic evidence [53] was the discovery that the electronic spectrum of a solution of [Nd(H2O)9](BrO3)3 was very similar to that of the crystalline material, known [12] to contain nine-coordinate [Nd(H2O)9]3+ ions, and quite distinct from that of species with different coordination numbers such as eight. It may be parenthetically remarked that this was possible for Nd3+, but for very few other lanthanides, as some of its absorption bands in the visible region of the spectrum exhibit ‘hypersensitivity’ to environment.
Other spectroscopic evidence includes information from hydration studies of lanthanide (III) ions by laser-induced fluorescence spectroscopy; combined with other techniques, it indicates a change in the hydration number from 9 to 8 in the Eu–Tb regions of the series [54,55]. A luminescence study [56] of lanthanide complexes revealed a linear correlation between the decay constant and the number of coordinated water molecules, this then being used to calculate first-coordination-sphere hydration numbers of 9.0, 9.1, 8.3 and 8.4 for Sm3+, Eu 3+, Tb3+, and Dy3+, respectively.
Among diffraction measurements, neutron-scattering measurements on the solutions of the aqua ions indicate a decrease in coordination number [57]. A neutron-diffraction study of Nd(ClO4)3 and Sm(ClO4)3 in solution indicates coordination numbers of 9.0 and 8.5 respectively, indicating that there are both eight and nine coordinate species present for samarium [58]. Values of ~7.9 have been obtained for Dy3+ and Lu3+; a molecular dynamics simulation study of lanthanide ions in aqueous solution showed that it was necessary to include allowance for polarization of the water molecule by lanthanide ions to get good agreement with this [59].
EXAFS, and related techniques such as XANES, are now starting to be applied to solutions of lanthanide compounds; thus EXAFS spectra of aqueous solutions of lanthanum perchlorate are in close agreement with that of solid [Ln(H2O)9] (CF3SO3)3, suggesting a coordination number of 9 for La3+(aq.) [60]. In an EXAFS study of chloride complexation by the lanthanides, hydration numbers of the aqua ions were deduced, values being 9.2 (La); 9.3 (Ce); 9.5 (Nd); 9.3 (Eu); 8.7 (Yb) and 9.7 (Y) [61]. A molecular dynamics simulation [62] for water exchange between [Sm(H2O)n]3+ ions and bulk water reveals very fast exchange between the bulk water and the hydrated samarium ion to maintain the equilibrium between [Sm(H2O)9]3+ and [Sm(H2O)8]3+. Monte Carlo simulations of Ln3+(aq) ions have been reported [63], agreeing with a change in coordination number from 9 to 8 in mid-series and with a dissociative substitution mechanism for the ennea-aqua ions.
In summary, in solution, the coordination number of [Ln(H2O)n]3+(aq) is believed to be 9 for the early lanthanides (La–Sm) and 8 for the later metals (Dy–Lu), with the intermediate metals exhibiting a mixture of eight and nine coordinate species. The nine-coordinate species are assigned tricapped trigonal prismatic structures and the eight-coordinate species square antiprismatic coordination.
3.1 Hydrated salts
As already noted, early (1939) studies [12] showed the existence of the [Ln(OH2)9]3+ ion in [Nd(H2O)9] (BrO3)3, and more recent studies have shown it to occur in a wide range of hydrated salts [Ln(OH2)9]X3 (X, e.g., bromate, triflate, ethylsulphate, tosylate). A series of triflates, [Ln(OH2)9](CF3SO3)3, (Ln = La–Nd, Sm–Dy, Yb, Lu), has been examined in detail [64]. Their structures resemble the corresponding bromates and ethylsulphates in being hexagonal, all containing the tricapped trigonal prismatic [Ln(OH2)9]3+ ion, even for the later lanthanides. The crystals of the triflate contain columns of [Ln(OH2)9]3+ cations and CF3SO3– ions, with the columns linked by a three-dimensional network of hydrogen bonds. This is presumably a factor that stabilises this structure and favours its isolation, even for the later lanthanides (Gd–Lu), where the eight-coordinate [Ln(OH2)8]3+ ion predominates in solution (as will be seen, this ion does crystallise with certain other counterions), and similar arguments are likely to apply to the ethylsulphates and bromates. The lanthanide–water distances for the positions capping the prism faces and at the vertices are, as expected, different. On traversing the series from La to Lu, the Ln–O distance decreases from 2.611 to 2.519 Å for the three face-capping oxygens but changes more steeply from 2.513 to 2.287 Å for the six apical oxygens [64]. An indication of the important role played by hydrogen-bonding forces in stabilising the structure of the hydrated triflates, is that even scandium, whose aqua ion appears to be pentagonal bipyramidal [Sc(OH2)7]3+ (5) [65] in solution, forms a [Sc(OH2)9]3+ ion in Sc(O3SCF3)3·9 H2O [66] 1 (Fig. 5).
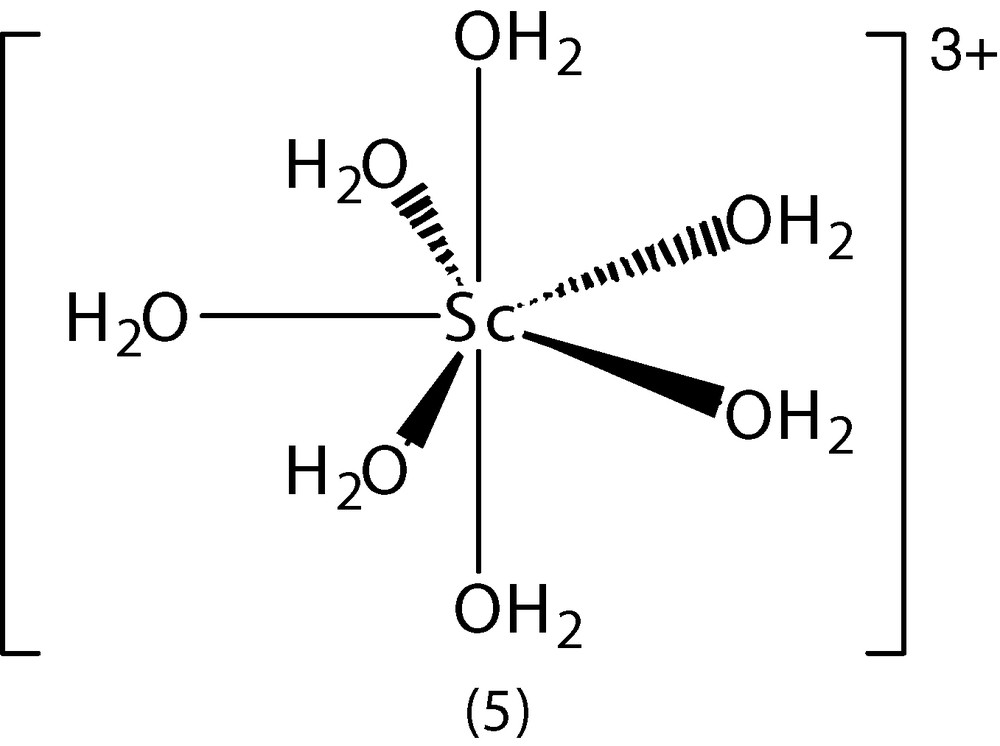
Structure of ion [Sc(OH2)9]3+ (5).
The series of ethylsulphates, [Ln(OH2)9](C2H5SO4)3, have been studied at 298 and 171 K more recently, with comparable results to the triflates [67]. The bromates and ethylsulphates each form isostructural series, both with hexagonal symmetry. The tricapped trigonal prisms have D3h symmetry in the bromates and C3h in the ethylsulphates. Again, the anions are hydrogen-bonded to the coordinated water molecules [68,69]. The ennea-aqua ion is also found in certain hydrated iodides, as recent diffraction studies [70] indicate that the iodides of the earlier metals are LnX3·9 H2O (Ln = La–Ho), containing the familiar tricapped trigonal prismatic [Ln(OH2)9]3+ ions. In comparison with the triflates and other complexes containing the tricapped trigonal prismatic nine-coordinate species, the spread of Ln–O distances is much smaller, falling in the range 2.552–2.576 Å for Ln = La and similarly between 2.403 and 2.405 Å for the holmium compound. The average Ln–O distance decreases from 2.55 Å (Ln = La) to 2.40 Å in the holmium compound. Coordinated water molecules all interact with iodide ions, not water molecules. For the heavier lanthanides, however, LnI3·10 H2O (Ln = Er–Lu) contain square antiprismatic [Ln(OH2)8]3+ ions; similarly, here the coordinated water molecules tend to have iodides for nearest neighbours, rather than hydrogen bonding to the lattice waters. No iodide ions are coordinated in either phase, unlike the lanthanide chlorides and bromides.
However, changing the counter-ion can have a more drastic effect upon the aqua species isolated. It has been known [71] for over 20 years that the hydrated lanthanide perchlorates Ln(ClO4)3·6 H2O contain octahedral [Ln(H2O)6]3+ ions in the solid state (Ln, e.g., La, Er, Tb). Again the anions are hydrogen-bonded to the coordinated waters.
Their isolation, however, must reflect a balance of factors such as solubility and hydrogen-bonding in the solid state, as there is a close similarity between the EXAFS spectra of aqueous solutions of lanthanum perchlorate and the spectrum of solid [Ln(H2O)9] (CF3SO3)3, indicating a coordination number of 9 for La3+(aq) in the perchlorate solutions [60].
3.2 Other hydrated salts
In other series, anion coordination occurs either for some metals or indeed throughout. Early lanthanides (La–Nd) form tosylate derivatives [Ln(OH2)9](p-MeC6H4SO3)3 with the usual trigonal prismatic coordination, but for the later lanthanide ions, the tosylate groups coordinate to the lanthanides in Ln(p-MeC6H4SO3)3·9 H2O, which contains [Ln(OH2)6(p-MeC6H4SO3)2]+ ions (Ln = Sm, Gd, Dy, Ho, Er, Yb, Y) in distorted dodecahedral eight-coordination [72]. Anion coordination occurs in all hydrated chlorides. The chlorides of La and Ce, LnCl3·7 H2O are dimeric [(H2O)7Ln(μ-Cl)2Ln(OH2)7]·Cl4 with what has been described as singly-capped square antiprismatic coordination of the metals, whilst LnCl3·6H2O (Ln = Nd–Lu) have square antiprismatic [LnCl2(H2O)6]+ ions with the coordinated chlorides on opposite sides of the polyhedron. There are extensive hydrogen bonding networks involving both coordinated and non-coordinated chlorides and water molecules [73].
Three different stoichiometries exist for the hydrated bromides. The heaviest lanthanides form LnBr3·8 H2O (Ln = Ho–Lu), which are [Ln(H2O)8] Br3, with no bromide coordinated, and which resemble a structure found in the hydrated iodides of the heavier lanthanides. Anion coordination is found for other metals, thus lanthanum and cerium form LnBr3·7 H2O, which are isomorphous with the corresponding chlorides in being dimeric [(H2O)7Ln(μ-Br)2Ln(OH2)7]·Br4. Hexahydrates LnBr3·6 H2O (Ln = Pr–Dy) again resemble heavier rare-earth chlorides in being [LnBr2(H2O)6]Br (though this resemblance does not extend to the end of the lanthanide series for the bromides). A comparison between corresponding chlorides and bromides indicates that the Ln–O distances, though shorter, show more sensitivity to the lanthanide contraction than the Ln-halogen distances [74].
A number of other salts have been shown to contain the octa aqua species. Thus [terpyH2]2[Tb(OH2)8]7Cl7· H2O contains [75] a ‘pure’ aqua ion formed even in the presence of a large excess of chloride ions. Other eight coordinate lanthanides are found in [Eu(OH2)8]2(V10O28)·8 H2O [76] and eight-coordinate ytterbium in ytterbium triflide, [Yb(OH2)8] [C(O2SCF3)2]3 [77]. Another such species is the [Lu(OH2)8]3+ ion, encapsulated inside a crown ether [Lu(OH2)8] Cl3·1.5 (12-crown-4)·2 H2O [78]. Similarly, the fact that erbium is eight coordinate (rather than six) in the dioxan solvate of erbium perchlorate, [Er(OH2)8](ClO4)3·(dioxan)·2 H2O shows the fine balance here [79]; another dioxan solvate, SmBr3·2 dioxan·9 H2O contains [Sm(OH2)9]3+ ions [80].
In the hydrated nitrates, there is a clear decrease in coordination number as the ionic radius of the lanthanide increases [81]. All nitrate groups are coordinated as bidentate ligands in these compounds, but the number of waters of crystallisation is no guide to how many are actually coordinated to the metal. Thus compounds Ln(NO3)3·6 H2O are known for La–Dy and Y. Of these, the lanthanum and cerium compounds are [Ln(NO3)3.(H2O)5]·H2O (Ln = La, Ce) with 11 coordinate lanthanides whilst the others are [Ln(NO3)3.(H2O)4]·2 H2O (Ln = Pr–Dy, Y) with 10-coordination for the metal. Under different conditions, a series of pentahydrates Ln(NO3)3·5 H2O is obtained (Ln = Eu, Dy–Yb), which also contains [Ln(NO3)3·(H2O)4] molecules. Lutetium forms Ln(NO3)3·4 H2O and Ln(NO3)3·3 H2O, isolated under very similar conditions, both of which contain nine-coordinate [Lu(NO3)3·(H2O)3] molecules [81].
Once again, the caveat applies that the stoichiometry of the material is not a guide to the molecular unit actually present. The overall picture is that, unlike the free aqua ions in aqueous solution, where the coordination number of the hydrated species is probably primarily determined by steric factors, in the solid state, other factors such as hydrogen bonding determine which species crystallizes. It may be that some (or all) of these factors operate in solution, and application of developing techniques may answer this point in the future.
3.3 The role of X-ray diffraction in resolving uncertainty in the number of coordinated solvent molecules
Apart from the hydrated salts discussed in section 3.2, there are many cases where ultimately the identity of the lanthanide-containing species can only ultimately be settled by X-ray diffraction. Thus reaction of aqueous lanthanide chlorides with alcoholic solutions of terpy (terpy = 2,2′:6′,2′′-terpyridyl) affords crystalline complexes Ln(terpy)Cl3·x H2O (Ln = La–Nd, x = 8; Ln = Sm, x = 7.6; Ln = Eu, x = 7.45; Ln = Gd, x = 7.1; Ln = Tb–Er, Yb–Lu, x = 7; Ln = Tm, Y, x = 6). They contain [Ln(terpy)Cl(H2O)n]2+ ions (Ln = La–Nd, n = 5; Ln = Sm-Lu, n = 4); this could not be deduced either from their stoichiometry or by any spectroscopic method [82]. Similarly, La(phen)3Cl3·9 H2O has been shown to be [La(phen)2(OH2)5]Cl3·4 H2O·phen [83], whilst La(phen)4(NO3)3·3 H2O is in fact [La(phen)2(H2O)2(NO3)2]NO3·2phen·H2O [84]. Sometimes small differences in stoichiometry that would not readily be detected by analysis, are revealed by crystallography. For example, crystals of two lanthanum nitrate complexes of 4-amino-bis(2,6-(2-pyridyl))-1,3,5-triazine (abptz), 10 and 11 coordinate [La(abptz)(NO3)3(H2O)n] (n = 1,2), can be isolated from the same reaction mixture, evidently because of similar solubilities [85]. This subtle difference in stoichiometry leads to significant differences in the molecular geometry. Thus, a comparison between the two lanthanum complexes shows the decrease in coordination number from 11 to 10 is accompanied by a decrease in La–O (water) distance from 2.589 (4) and 2.610 (4) Å to 2.483 (5) Å; similarly, the La–N distances decrease from 2.739 (4), 2.755 (5) and 2.805 (6) in the 11-coordinate compound to 2.576 (5), 2.625 (5) and 2.641 (5) Å in 10-coordinate [La(abptz)(NO3)3(H2O)]. The range of La–O (nitrate) distances decreases from 2.628 (4)–2.702 (5) Å, with an outlier at 2.805 (6) Å in [La(abptz)(NO3)3(H2O)2], to 2.525 (5)–2.620 (5) Å in [La(abptz)(NO3)3(H2O)], indication of congestion in the coordination sphere in the 11-coordinate complex. Other examples of this are referred to in this article, notably the complexes of the lanthanide nitrates with terpyridyl, discussed in section 4.5
4 More studies of the ‘lanthanide contraction’
Other series of simple lanthanide complexes have been studied in some detail; occasionally the coordination number stays unchanged across the series from La to Lu, most usually not.
4.1 Tetrahydrofuran complexes of the lanthanide chlorides
A range of stoichiometries is known, and the formulae and structures of these complexes present considerable diversity. Five different stoichiometries of LnCl3(thf)x (x, e.g. 2, 2.5, 3, 3.5, 4) and six different structure types have been identified in these complexes (Table 1). The compound obtained not only depends upon the lanthanide and the reaction stoichiometry but upon reaction conditions [86,87]. The pattern across the series reflects an overall decrease in coordination number from 8 (La) to 6 (Lu). Lanthanum uniquely forms [LaCl3(thf)2] which has a single-stranded polymer ...La(μ-Cl)3(thf)2La(μ-Cl)3(thf)2La... with cis-thf molecules and square antiprismatic eight-coordination of lanthanum [86]. [LnCl3(thf)2] (Ce–Nd) are different, although again polymeric, in this case seven coordinate ...LaCl(thf)2(μ-Cl)2LaCl(thf)2(μ-Cl)2... chains. A third type, found for Nd–Gd, are monomeric seven coordinate [LnCl3(thf)4], whilst Gd–Tm form a nominal [LnCl3(thf)3.5], which in fact has an ionic structure [LnCl2(thf)5]+ [LnCl4(thf)2]–, containing a seven coordinate cation and octahedrally coordinated six coordinate anion, both with trans geometries. Ytterbium forms a dimeric [Cl2(thf)2Yb(μ-Cl)2Yb(thf)2Cl2], whilst both ytterbium and lutetium form a monomeric octahedral mer- [LnCl3(thf)3] (Ln = Yb, Lu), a type long familiar with scandium.
Structure types characterized for lanthanide chloride complexes of thf
| La | Ce | Pr | Nd | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu |
| 1 | 2 | 2 | 2,3 | 3 | 3 | 3,4 | 4 | 4 | 4 | 4 | 4 | 5,6 | 6 |
4.2 Alkyls with the CH2SiMe3 ligand
The alkyls [Ln(CH2SiMe3)3(thf)n] (n is probably 3) appear to be very unstable for lanthanides larger than samarium, but [Sm(CH2SiMe3)3(thf)3] has been shown to have a fac-octahedral structure [88], as does [Y(CH2SiMe3)3(thf)3] [89]. However, [Ln(CH2SiMe3)3(thf)2] (Ln = Er, Yb, Lu) all have five coordinate trigonal bipyramidal structures [88]. In addition to these compounds, [Y(CH2SiMe3)3(thf)2] and [Er(CH2SiMe3)3(thf)3] have received thorough non-crystallographic characterisation [90,91], so it appears that both five- and six-coordinate species exist in equilibrium (depending upon thf concentration) in solution and are both isolable in the solid state for certain lanthanides.
4.3 2,2'-bipyridyl (bipy) complexes of the lanthanide nitrates
Within the series Ln(bipy)2(NO3)3 (Ln = Y, La–Lu except Pm) all the structures reported thus far (Ln = La, Pr, Nd, Eu, Lu [92–94]) are isomorphous and have 10-coordinate lanthanides with all nitrates present as bidentate ligands; these thus appear to be an example of the coordination number remaining constant across the series, despite a 16% decrease in ionic radius of the lanthanide ion. The coordination geometry has been variously described as a bicapped dodecahedron and as a sphenocorona, indicating, as do results for many other systems, that distortions of the coordination sphere from regular polyhedral geometries are readily achieved for the lanthanides, when two or more different ligands are present in the coordination sphere. In addition, a number of compounds Ln(bipy)3(NO3)3 (Ln = Ce, Pr, Nd, Yb) have been reported, the neodymium complex being shown to be [Nd(bipy)2(NO3)3]·bipy, with the third bipy molecule not associating with the neodymium-containing complex [95]. In the presence of certain crown ethers, other molecular units have been stabilised however. In the presence of 15-crown-5, reaction of lanthanum nitrate with bipy in MeOH–MeCN led to [La(bipy)(NO3)3(H2O)2(MeOH)]·15-crown-5, which has 11-coordinate lanthanum [96]. The increase in coordination number in comparison with [La(bipy)2(NO3)3] results in a slight (and possibly not statistically significant) increase in La–N distance from 2.66 Å to 2.70 Å, and in La–O from 2.56–2.63 Å to 2.69 Å. The presence of the coordinated MeOH molecule supplies a fifth hydrogen atom, so that hydrogen bonds can be formed to all the crown ether oxygens (which do not coordinate to the lanthanide). In another synthesis in the presence of a crown ether, a 10-coordinate complex, [La(bipy)(NO3)3(H2O)2]·benzo-15-crown-5, is obtained [97].
4.4 1,10-phenanthroline (phen) complexes of the lanthanide nitrates
Another family with the coordination number remaining constant across the series, is [Ln(phen)2(NO3)3], which broadly resemble the bipy complexes, having three bidentate nitrate groups and 10 coordinate lanthanide. Again the complexes appear to form an isomorphous and isostructural series [92]. On moving from the lanthanum to the lutetium compound, the Ln–N distances decrease from 2.646 (3)–2.701 (3) Å (La) to 2.462 (8)–2.479 (8) Å (Lu), and the range of Ln–O distances decreases from 2.580 (3)–2.611 (3) Å for the lanthanum, compound to 2.364 (8)–2.525 (6) Å for the lutetium complex. The individual complex molecules associate by π−π stacking into one dimensional chains which themselves arrange into pseudo 1D close packed patterns [98]. It may be that it is the ability of the bidentate ligands in these and the bipy analogues to ‘mesh’ in the coordination sphere (and in the case of phenanthroline to interact through π−π stacking) that is responsible for the constancy of coordination number in these series. The ability of the planar 1,10-phenanthroline molecule to associate by π−π stacking appears widespread in lanthanide complexes, and can involve both coordinated and uncoordinated phen, the latter not infrequently appearing as a ‘phenanthroline of crystallization’ in the lattice.
4.5 2,2':6',2”-terpyridyl (terpy) complexes of the lanthanide nitrates
These show a wide range of structures, even within the 1:1 terpy: lanthanide stoichiometry, depending upon the solvent used in the synthesis.
The only detailed solution study [99] involved addition of terpy to a solution of La(NO3)3·6 H2O in MeCN, followed by 1H, 17O and 139La NMR. A number of species were identified present in solution, namely [La(terpy)(NO3)3(MeCN)], [La(terpy)(NO3)3(H2O)], [Ln(terpy)(NO3)4(MeCN)]–, [Ln(terpy)(NO3)4(H2O)]- and [Ln(terpy)2(NO3)2]+. Reaction of the lanthanide nitrates with 1 mol of terpy in MeCN exhibits predictable behaviour in the complexes isolated, [100] in that the smallest metal ions form water-free 9-coordinate [Ln(terpy)(NO3)3] (Ln = Ho-Lu), the slightly larger lanthanides form 10-coordinate [Ln(terpy)(NO3)3(H2O)] (Ln = Ce–Dy) and only lanthanum forms 11-coordinate [La(terpy)(NO3)3(H2O)2]. All of these complexes feature bidentate nitrate groups, showing the important and widespread ability of this small-bite bidentate ligand to form complexes with the lanthanides. Under slightly different conditions of stoichiometry (Scheme 1), [Ln(terpy)(NO3)3(H2O)]·terpy (Ln = Ho, Er, Tm, Yb) have been obtained [101]. Reaction of yttrium nitrate with terpy in MeCN yields two yttrium complexes [102]. Reaction with 2 mol of terpy in MeCN followed by crystallisation gave crystals of nine-coordinate [Y(terpy)(NO3)3(H2O)]·terpy·3 MeCN, which contains two bidentate and one monodentate nitrate groups, whilst layering of more dilute solutions with ether formed [Y(terpy)(NO3)3(H2O)], with ten-coordinate molecules with three bidentate nitrates.

Formation of variously solvated terpyridine complexes of thulium nitrate.
Unlike the early lanthanides, where the same complex is obtained from synthesis in either acetonitrile or ethanol, solvent affects the structure for the 1:1 complexes of later lanthanides. Reaction of hydrated lanthanide nitrates with terpy in ethanol affords [Ln(terpy)(NO3)3.(C2H5OH)] (Ln = Dy–Lu, Y), which contains both bidentate and monodentate nitrates as well as a coordinated ethanol [103,104]. The lanthanide is nine-coordinate in these complexes. Two nitrates are bidentate, with Ln–O distances some 0.14 Å longer than that of the Ln–O bond involving the unidentate nitrate. A second oxygen in this unidentate nitrate is hydrogen-bonded to the coordinated ethanol molecule. As already noted, reaction of later lanthanide nitrates with terpy in MeCN solution affords 9-coordinate [Ln(terpy)(NO3)3]. Solvolysis of a nitrate group in [Yb(terpy)(NO3)3] is stereoselective, the nitrate trans- to the terpy ligand being replaced by ethanol and by water, with the formation of [Yb(terpy)(NO3)3(EtOH)] (which has one unidentate nitrate) and [Yb(terpy)(NO3)2(H2O)2]NO3·2 H2O respectively. A similar effect is noted in the lutetium analogue with the isolation of an unusual complex [Lu(terpy)(NO3)2(H2O)(EtOH)](NO3), where both water and ethanol are bound to lutetium in preference to nitrate coordination, as well as the ethanol solvate [Lu(terpy)(NO3)3(EtOH)]. In [Lu(terpy)(NO3)3], Lu–N distances are 2.379–2.407 Å and Lu–O bonds fall into the range 2.350–2.440 Å, so that even with the smallest lanthanide, all the nitrates are essentially bidentate. Replacement of a bidentate nitrate trans- to the terpy by a coordinated ethanol and a unidentate nitrate causes a certain reorganisation in the coordination sphere, with Lu–N bonds increasing by about 0.06 Å; the Lu–O (water) distance is 2.279 (3) Å and the Lu–O(ONO2) distance is 2.279 (3) Å, showing that the Lu–O bond is about 0.1 Å shorter than for an oxygen atom in a bidentate nitrate group. Scheme 2 shows how small changes in conditions affect the lutetium complex isolated.
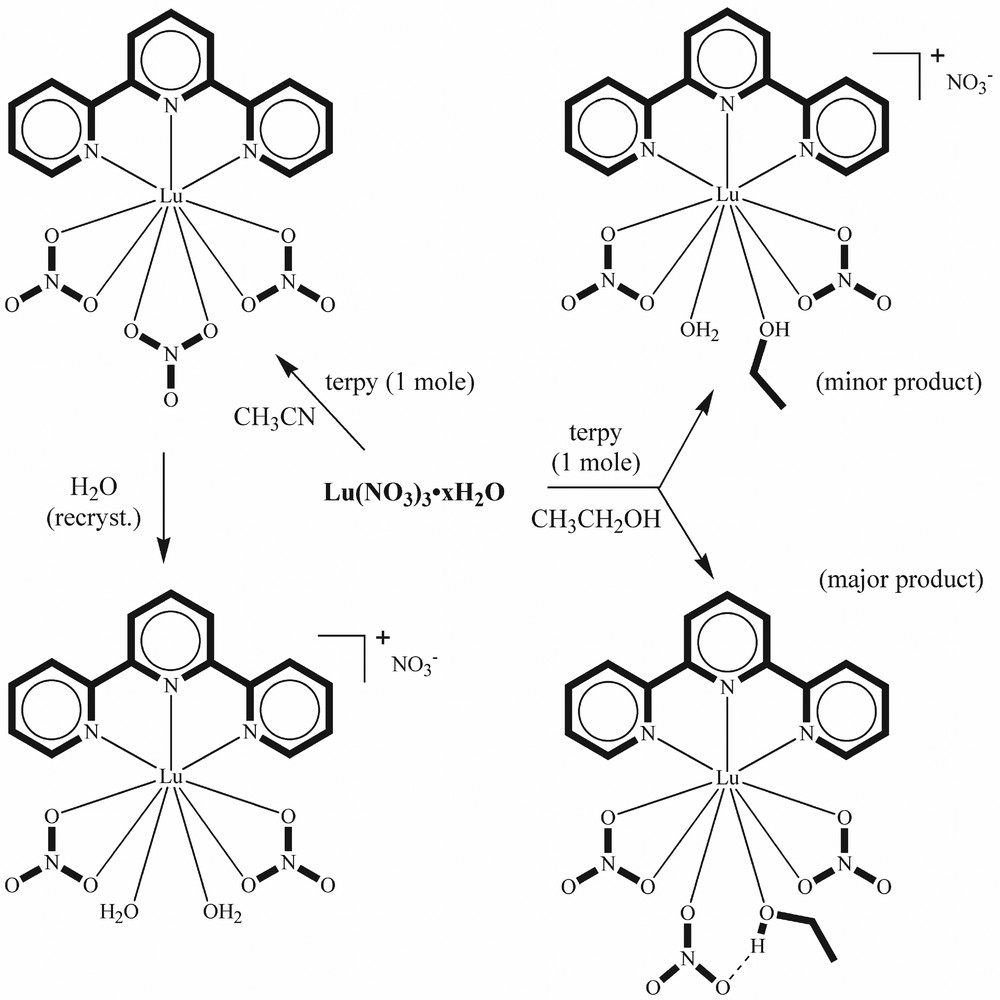
Formation of terpyridine complexes of lutetium nitrate.
In another study, spanning the lanthanide series, Semenova and White [105] reacted lanthanide nitrates with terpy in MeCN, then recrystallised the products from water. They found that the earlier members of the lanthanide series form 10-coordinate [Ln(terpy)(NO3)2(H2O)3] NO3 (Ln = La-Gd) and the later lanthanides form 9-coordinate [Ln(terpy)(NO3)2(H2O)2] NO3·2 H2O (Ln = Tb–Lu, Y). These compounds presumably result from solvolysis by water of an initial [Ln(terpy)(NO3)3(H2O)x] species, displacing one nitrate group, as such replacements with other solvent molecules have been noticed in the case of the Yb and Lu complexes discussed earlier. Detailed structures have been reported for the La, Gd, Tb, Lu and Y complexes. They show a girdle of ligands comprising a virtually planar terdentate terpy ligand and two or three water molecules coordinated round the ‘waist’ of the metal, with bidentate nitrates completing the coordination sphere above and below the metal; alternatively, in comparison with the [Ln(terpy)(NO3)3] complexes, the nitrate group trans- to terpy has been replaced by the water.
Reaction of the hydrated nitrates (Ln = La, Ce) with terpy in MeOH results in crystals of two methanol complexes (these are not isolated for Pr and later lanthanides).
The 11-coordinate [La(NO3)3(terpy)(MeOH)2] has been isolated from the reaction of lanthanum nitrate with terpy in methanol, the lanthanum being 11-coordinate, with three bidentate nitrates, the La–N distances being 2.688 (3), 2.700 (3) and 2.715 (3) Å. Five of the La–O (nitrate) distances span 2.596 (3)–2.727 (3) Å, the sixth being a rather longer 2.926 (3) Å; La–O (methanol) bonds are 2.560 (2) and 2.580 (2) Å [105]. The isomorphous Ce analogue shows similar evidence for steric congestion [106]. The ‘long’ lanthanide–oxygen bonds involving some nitrate groups, in the range between 2.8 to over 2.9 Å and some 0.3 Å longer than the others, raise questions about the strength of the interaction and the extent to which the oxygen is ‘coordinated’ to the metal.
Overall, a wide range of 1:1 complexes is known, though the picture is not yet complete, and some findings have yet to be reported. The role of solvent is critical in these syntheses.
4.6 Lanthanide acetates
The structures of the anhydrous acetates have been discussed in a series of papers. Anhydrous lanthanum acetate [107] contains ten coordinate lanthanum, involving both chelating and bridging acetates, the latter having one oxygen bound to two different lanthanum ions and the second oxygen just bound to one lanthanum. La–O distances lie in the range 2.474 (3) to 2.794(3) Å, with an average of 2.615 Å. Ce(CH3COO)3 is isostructural. Both 9- and 10-coordinate praseodymium are found in Pr(CH3COO)3 [108]. For the two types of nine-coordinate Pr sites, the average Pr–O distances are 2.535 and 2.556 Å, whilst for the 10-coordinate site, the average Pr–O distance is 2.611 Å. Like La(CH3COO)3 this has a three-dimensional network structure, whereas the later metals adopt chain structures in Ln(CH3COO)3. Holmium acetate adopts a structure shared with other Ln(CH3COO)3 (Ln = Sm–Er, Y). Here holmium occupies two slightly different 8-coordinate sites, with average Ho–O distances of 2.370 and 2.381 Å. Ln(CH3COO)3 (Ln = Tm–Lu) have the structure exemplified by Lu(CH3COO)3, in which Lu is 7-coordinate (average Lu–O 2.275 Å). On heating, both these structures change to the six-coordinate Sc(CH3COO)3 structure, this drop in coordination number being accompanied by an acetate group switching to a symmetrical bridging mode [109]. The coordination number of the lanthanide thus drops from 10 to 7 across the series. Acetate and nitrate, both small ‘bite’ species exhibit some similarities as ligands in lanthanide complexes, but these should not be pressed too far, as the ability of carboxylates to form asymmetric bridges does not seem to be emulated by nitrate.
5 The influence of counter-ion on the complex isolated
5.1 Thiocyanate complexes
Recent extensive studies have shown that the stoichiometry and structure of the anionic complex obtained depends greatly upon factors such as the counterion used and upon the solvent employed. These compounds are generally made by reaction of the lanthanide thiocyanate with the alkylammonium thiocyanate in a suitable solvent (e.g., an alcohol) or mixture of solvents. [NEt4]3 [Ln(NCS)6]·solvent (M = Er,Yb; solvent = C6H6, C6H5F, C6H5Cl, C6H5CH3) have octahedrally coordinated lanthanides [110]; [NBun4]3[Ln(NCS)6] (M = Y, Pr–Yb) are also known to contain 6-coordinate lanthanides, confirmed by a diffraction study of the neodymium compound [111]. Reaction of lanthanide thiocyanates with tetramethylammonium thiocyanate in methanol-water, followed by slow crystallisation, gives [NEt4]4[Ln(NCS)7(H2O)] (Ln = La–Nd, Dy, Er) which have a cubic 8-coordinate geometry round the lanthanides [112]. Reaction of NEt4NCS with the lanthanide thiocyanate in MeOH/water followed by vapour diffusion of benzene into the initial water/methanol mixture, affords [NEt4][Ln(NCS)4(H2O)4] (Ln = Nd, Eu) with square-antiprismatic coordination [113]. In contrast, if the water is removed by forming an azeotrope with benzene/ethanol followed by vacuum evaporation, then by crystallisation of a methanolic solution in benzene vapour, crystals of [NEt4]4[Ln(NCS)7]·benzene (Ln = La, Pr) are obtained, which have a capped trigonal prismatic geometry, not involving the lattice benzene molecule [114]. If the lanthanide thiocyanates are reacted with NMe4NCS in methanol–water, followed by slow crystallisation, this usually affords [NMe4]3·[Ln(NCS)6(MeOH)(H2O)] (Ln = La–Nd, Sm–Dy, Er), which have square antiprismatic coordination of the lanthanides. If the synthesis is carried out in a water free-environment, [NMe4]4 [Ln(NCS)7] (Ln = Dy, Er, Yb) are obtained; these have a coordination geometry most closely approximating to a pentagonal bipyramid [115].
Crystallisation of a methanolic solution of NMe4NCS and the lanthanide thiocyanates in benzene vapour gives crystals of [NMe4]5[Ln(NCS)8]·2 C6H6 [116].
5.2 EDTA complexes
The pattern of solid-state structures of lanthanide EDTA complexes previously determined is that there is a change in the number of coordinated waters from 3 to 2 near the end of the series, following the lanthanide contraction. Na[Ln(EDTA)(H2O)3]·5 H2O (Ln = La–Dy) are isostructural, with 9-coordinate lanthanides, as do K [Ln(EDTA)(H2O)3] (Ln = La, Nd) [117]. K[Yb(edta)(OH2)2]·5 H2O and Cs [Yb(edta)(OH2)2]·5 H2O contain 8-coordinate ytterbium [118]. Structures of several M[Ln(edta)(H2O)]n] (M = alkali metal; Ln = lanthanide) show that the coordination number depends upon the ionic radii of both the lanthanide and the alkali metal [119].
Thus, Cs[Dy(edta)(OH2)2]·3 H2O and Cs[Ho(edta)(OH2)2]·3 H2O have eight coordinate lanthanides, whilst Na[Er(edta)(OH2)3]·5 H2O, K[Ho(edta)(OH2)3]·2 H2O, Cs [Nd(edta)(OH2)3]·3.5 H2O, Cs[Sm(edta)(OH2)3]·4 H2O and Cs[Gd(edta)(OH2)3]·4 H2O all have nine coordinate lanthanides. Evidently there is a region towards the end of the lanthanide series where the eight and nine coordinate anions have similar stabilities, and it is the solubility of the compound that determines which is isolated.
6 The influence of weak forces in the pyramidal structures of the alkyls and alkylamides
The amides [Ln((CH(SiMe3)2)3] (Ln = La–Lu) and alkyls [Ln((CH(SiMe3)2)3] (Ln = La, Sm) have long been known to have severely distorted three coordinate trigonal pyramidal structures [26–28, 32]. Whilst [Ln{N(SiMe3)2)3] do not form isolable thf adducts (though [{Ln{N(SiMe3)2)3}(Ph3PO)] [29] and [Ln(N(SiMe3)2)3(CyNC)2] exist [30] trigonal bipyramidal [Ln(N(SiHMe2)2)3] form five-coordinate [Ln(N(SiHMe2)2)3(thf)2], (Ln = Y, La–Lu) are isostructural, another case where a series of compounds exhibiting the same coordination number exists across the whole lanthanide block [120]. The use of less bulky ligands, often fluorinated, has permitted the study of several interesting species, thus in [Sm(N(SiMe3)(C6F5))3] there are many Sm···F and agostic interactions (6) [121] (Fig. 6).
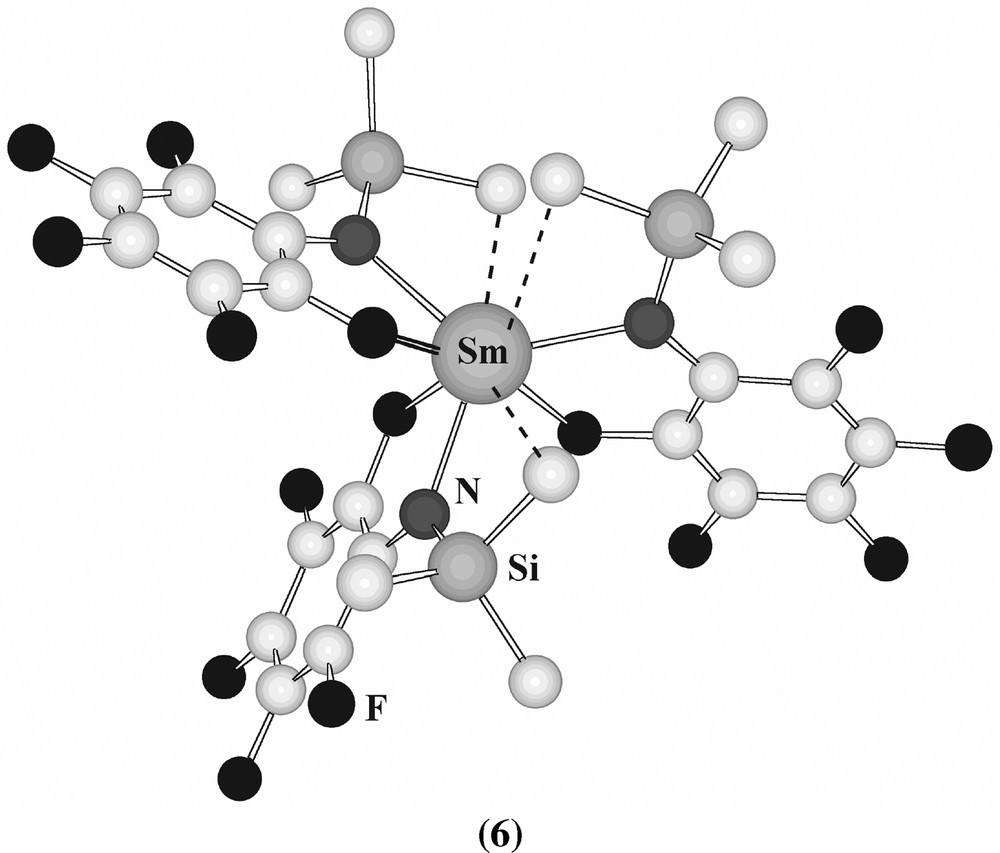
Structure of [Sm(N(SiMe3)(C6F5))3] (6).
[Sm(N(C6F5)(SiMe3))3(thf)] (7) has distorted tetrahedral coordination of samarium, but with additional close Sm···F contacts and an ‘agostic’ Sm–C contact [122] (Fig. 7). The amide [Er{NBut(SiMe2H)}3], which has an unexpectedly high vapour pressure, displays three agostic Er-H-Si interactions in the solid state [123]. [(η6-C6H5Me)Nd(N(C6F5) 2)3] has a η6-bonded toluene molecule with a distorted piano-stool geometry [121].
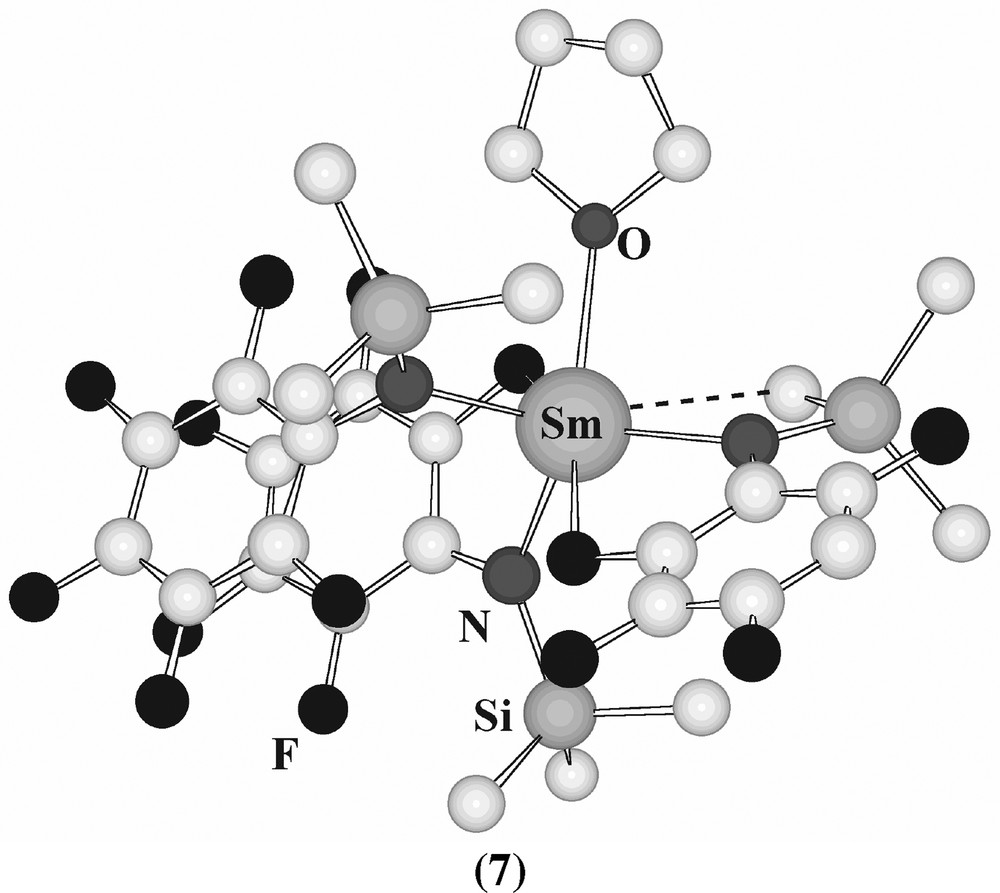
Structure of [Sm(N(C6F5)(SiMe3))3(thf))] (7).
Recent Density Functional Theory calculations on the model alkyls [Ln((CH(SiRR’2)(SiR3))3] (R = R′ = Me; R = H, R' = Me; R = R' = H) and [La(CH3)3] indicate that lengthened Si–C bonds are associated with β-Si–C agostic interactions, whereas the hitherto favoured γ C–H agostic interactions are in fact repulsive and in fact lead to hardly any changes. The key features were reproduced by model such as [Ln(CH(SiMeH′2)(SiH3))3]; in [Ln((CH(SiH3)2)3], the β-Si–C interactions are replaced by β-Si–H interactions [124,125].
Examination of the crystal structure [28] of [Sm{(N(SiMe3)2)3}] (8) shows that one methyl group in each amide is placed above the pyramid relatively close to the samarium (Sm–C 3.003(4) Å; compare Sm–N 2.284(3) Å) suggesting the presence of agostic interactions (Fig. 8). DFT calculations on it support this view, again indicating the presence of β-Si–C agostic interactions.
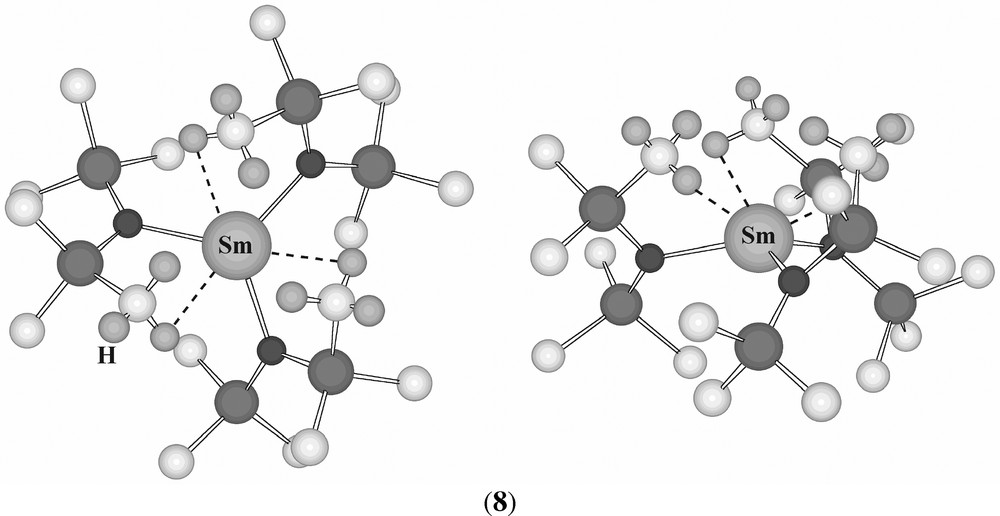
‘Overhead’ (left) and ‘side’ (right) views of (8), with hydrogen atoms shown only on the methyl groups involved in the closest approach to the metal. Sm···H = 2.80 Å.
7 Conclusions
Lanthanide coordination chemistry has matured to the stage where its rich variety of coordination numbers [20, 126] is taken for granted; now it is starting to be realised that the existence of a particular species in solution and its isolation in the solid state is the product of a number of small factors. The examination of the structures of lanthanide complexes in the solid state has indicated that, in the absence of the strong directional forces that often dictate coordination geometries in transition metal complexes, other factors become important in determining the species formed, including the steric bulk of the ligand (e.g., alkoxides, alkylamides and hydrocarbyls); the role of the counter-ion in dictating the ion to crystallize (hydrated salts, thiocyanate and EDTA complexes); the possibility of hydrogen bonding being influential, whether in hydrated salts or in stabilizing unusual geometries of the nitrate group (terpy complexes); the role of π-interactions involving the ligand (aryloxides, phen complexes); and agostic interactions favouring a particular geometry (silylamides and related species). The understanding of these factors is still developing. Water is undoubtedly an important ligand, but 40 years of studying complexation in non-aqueous solvents has led to a rich range of complexes using other donor atoms, so that the tendency to see the lanthanide ions as being oxophilic needs to be qualified.
As far as the structure of lanthanide complexes in solution is concerned, the position is perhaps analogous to that of solid-state structures some 35 years ago. Application of EXAFS and related techniques is starting to yield interesting information, but at present there is a need for the techniques to be refined so that different ligands and donors in the same coordination sphere can be readily distinguished.
Acknowledgements
I am greatly indebted to Paul Raithby and John Fawcett for their collaboration in some of the research discussed here, also to Jack Harrowfield for his very considerable assistance in the preparation of this article.
1 Note there is recent evidence that the cation present in the solid is actually [Sc(OH2)8]3+ – see P. Lindqvist-Reis, Structure of Solvated Metal Ions, doctoral thesis, Royal Institute of Technology (KTH), Stockholm, Sweden, 2000. http://www.lib.kth.se/Sammanfattingar/reis000614.pdf.


