1 Introduction
There is contemporary growing interest in the chemistry of paramagnetic compounds due to their potential applications as magnetic materials [1–4]. Since the discovery of the [Mn12O12(OAc)16(H2O)4] {Mn12} as the first single-molecular magnet (SMM) [5,6], the quest had been opened for polynuclear metal complexes with ever larger spin ground states [7]. This is based on the fact, that the slow relaxation of the magnetic moment is a crucial condition and is related to the anisotropy barrier U of the system, which depends on the total spin S and the easy-axis anisotropy parameter D with U = |D|S2 for integer and U = |D|S2–1/4 for half-integer spins. In this context rational design strategies have been developed leading to parallel spin alignment with the spin-polarization mechanism as a commonly employed recipe [8]. Although this approach allows the implementation of symmetry conditions that are advantageous as the magnetic relaxation behavior of the resulting complexes is concerned, it is unfortunately not strictly leading to ferromagnetic coupling between the metal centers [9–13].
However, in recent years the focus in the search for new SMMs has been shifted from optimizing the total spin S towards the creation of systems with larger |D|, i.e. increasing the local zero-field splitting (ZFS) parameters in the system, as it has been recognized that the anisotropy barrier U is virtually independent of S [14,15]. This has already led to significant advances for polynuclear systems [16–19]. Recently, it has been shown that SMM behavior can also be observed for mononuclear complexes. Beside lanthanide based systems [20–24] also 3d metal ions came into focus, i.e. iron(II) [25–27] and cobalt(II) complexes [28,29].
In general the magnetic relaxation of SMMs is not solely governed by the thermal relaxation process determined by the anisotropy barrier U, as additional quantum tunneling of magnetization (QTM) plays an important role which leads to relaxation even at temperatures well below those corresponding to the thermally accessible barrier [4]. It is therefore of major interest to control the QTM process in SMMs for potential future applications in fields like molecular spintronics, information storage, and quantum computing [30–34]. Besides dipolar and hyperfine interactions the transverse anisotropy (E) is responsible for resonant QTM at zero field. The latter can be avoided by utilizing half-integer spin systems, as the mixing of ± MS levels by E is forbidden according to Kramers’ theorem [35].
We therefore started to explore high-spin cobalt(II) complexes possessing an S = 3/2 ground state in order to find systems with appropriate magnetic properties. Such systems with tetrahedral coordination geometry generally show a considerable ZFS [36–39] which strongly depends on the distortion from the ideal Td symmetry [40]. Studies on 2-(1H-imidazol-2-yl)phenol based ligands and their zinc(II) and nickel(II) complexes have shown that these ligands support neutral complexes with tetrahedral coordination geometry [41–43]. Herein, we describe the synthesis and magnetic characterization of a series of new mononuclear cobalt(II) complexes based on 2-(1H-imidazol-2-yl)phenol ligands.
2 Experimental
2.1 Materials and instrumentation
Abbreviations used throughout the text:
- • L1 = 2-(4,5-diphenyl-1H-imidazol-2-yl)phenol;
- • L2 = 2-(4,5-diphenyl-1H-imidazol-2-yl)-4-nitrophenol;
- • L3 = 2-(4,5-diphenyl-1H-imidazol-2-yl)-6-methoxyphenol.
All starting materials were obtained commercially as reagent grades and used without further purification. The 2-(1H-imidazol-2-yl)phenol based ligands were prepared according to recently published procedures [42]. The synthesis of complex [Co(L1)2] (1) was initially described by MacDermott [44]. IR spectra were recorded on a Bruker Equinox spectrometer with a diamond ATR unit in the range of 4000 to 370 cm−1. Elemental analyses were performed on a Leco CHNS-932 or El Vario III elemental analyzers.
2.2 Synthesis of the complexes
The cobalt(II) salt and the ligand were dissolved in 10 mL ethanol and stirred at reflux for 30 minutes. The reaction mixture was cooled to room temperature and the product isolated by filtration. The orange-pink polycrystalline samples were washed with a few milliliters of ethanol and dried overnight in a desiccator over silica at room temperature.
2.2.1 [Co(L1)2] (1)
Cobalt acetate(II) tetrahydrate (174 mg, 0.72 mmol), 2-(4,5-diphenyl-1H-imidazol-2-yl)phenol (451 mg, 1.44 mmol); yield 550 mg (0,71 mmol, 99%). Anal. calc. for C46H42CoN4O4 (1·2EtOH); M.wt. (773.76): C, 71.41; H, 5.47; N, 7.24. Found: C, 71.39; H, 5.57; N, 7.28. IR: 3060(w), 2970(w), 1605, 1477(m), 1452(m), 1307(m), 1245, 1144, 1045, 855, 765(s), 752(m), 694(s), 609, 506, 464, 434 cm−1.
2.2.2 [Co(L2)2] (2)
Cobalt(II) acetate tetrahydrate (58 mg, 0.24 mmol), 2-(4,5-diphenyl-1H-imidazol-2-yl)-4-nitrophenol (234 mg, 0,65 mmol); yield 181 mg (0,23 mmol, 96%). Anal. calc. for C42H28CoN6O6 (2); M.wt. (771.66): C, 65.37; H, 3.66; N, 10.89. Found: C, 64.81; H, 3.81; N, 10.95. IR: 3246(w), 3055(w), 1603, 1563, 1484(s), 1302(s), 1272(s), 1128(s), 887, 832, 767, 752, 739, 694(s), 659, 625, 586, 506, 460 cm−1.
2.2.3 [Co(L3)2] (3)
Cobalt(II) acetate tetrahydrate (47 mg, 0.19 mmol), 2-methoxy-6-(4,5-diphenyl-1H-imidazol-2-yl)phenol (182 mg, 0.53 mmol); yield 132 mg (0,18 mmol, 95%). Anal. calc. for C46H40CoN4O5 (3·EtOH); M.wt. (787.78): C, 70.13; H, 5.12; N, 7.11. Found: C, 69.81; H, 5.18; N, 7.26. IR: 3065(w), 2962(w), 2830(w), 1604(w), 1474(s), 1445, 1391, 1322, 1235(s), 1214(s), 1196, 1179, 1074(s), 857, 836, 766(s), 740, 728, 695(s), 637, 582, 510, 455 cm−1.
2.3 Magnetic measurements
The magnetic properties were measured on a Quantum Design MPMS-5 SQUID Magnetometer in the temperature range from 300 to 2 K at static fields up to 5 T. The polycrystalline samples were mounted in gel capsula. The data were corrected for the diamagnetism of the sample holder and capsula as well as for the diamagnetic contribution of the ligand. Measurements of the ac susceptibility were performed with an alternating field of 3 Oe at constants dc fields of 0, 400, and 1000 Oe in the frequency range of 10 to 1500 Hz and at temperatures from 2 to 15 K. The experimental data were fitted for each temperature to Eq. (1). This allows one to extract the adiabatic and isothermal susceptibility (χs and χ0), the magnetization relaxation time (τc) and the distribution width (α) using OriginPro 8.5:
| (1) |
2.4 Crystal structure analyses
Single crystals for complexes 1 and 2 were obtained by recrystallization from MeOH and DMF, respectively. Suitable crystals were selected while covered with mother liquor under a polarizing microscope and fixed on fine glass fibers. The crystallographic data was collected on a Nonius KappaCCD diffractometer using graphite-monochromated Mo-Kα radiation (λ = 71.073 pm). A summary of crystallographic and structure refinement data is given in Table 1. Data were corrected for Lorentz and polarization effects, but not for absorption effects. The structures were solved by direct methods with shelxs-97 and refined by full-matrix least-squares techniques against
Summary of the crystallographic and structure-refinement data for compounds [Co(L1)2].3MeOH (1.3MeOH) and [Co(L2)2].2.5DMF (2.2.5DMF).
| Compound | 1.3MeOH | 2.2.5DMF |
| Empirical formula | C45H42CoN4O5 | C49.5H45.5CoN8.5O8.5 |
| Formula weight | 777.76 | 954.37 |
| Crystal size (mm) | 0.5 × 0.5 × 0.5 | 0.8 × 0.5 × 0.5 |
| Crystal system | monoclinic | monoclinic |
| Space group | P21/c | C2/c |
| a (pm) | 1963.62(4) | 3618.24(7) |
| b (pm) | 2630.85(6) | 1532.45(4) |
| c (pm) | 1561.92(3) | 16.2967(4) |
| β (°) | 109.4760(10) | 100.091(2) |
| V (nm3) | 7.6072(3) | 8.8964(4) |
| Z | 8 | 8 |
| Dcalcd (g cm−3) | 1.358 | 1.425 |
| μ (mm−1) | 0.504 | 0.454 |
| θ range of data collection (°) | 2.08, 27.49 | 2.36, 27.48 |
| Measured reflections | 41808 | 26227 |
| Unique reflections (Rint) | 17305 (0.0731) | 10160 (0.0534) |
| Goodness-of-fit on F2 | 1.149 | 1.091 |
| R1(I>2σ(I))a | 0.0788 | 0.0623 |
| wR2 (all data, F02)b | 0.1495 | 0.1348 |
a R1 = ∑||Fo|–|Fc||/∑|Fo|
b wR2 = [∑w(Fo2–Fc2)2/∑w(Fo2)2]1/2
3 Results and discussion
3.1 Synthesis
The 2-(1H-imidazol-2-yl)phenol based ligands 2-(4,5-diphenyl-1H-imidazol-2-yl)phenol (L1), 2-(4,5-diphenyl-1H-imidazol-2-yl)-4-nitrophenol (L2), and 2-(4,5-diphenyl-1H-imidazol-2-yl)-6-methoxyphenol (L3) depicted in Scheme 1 are employed in the synthesis of complexes.
The reaction of cobalt(II) acetate tetrahydrate in ethanol solution with the ligands L1, L2, and L3 results in the formation of the corresponding neutral cobalt(II) complexes with a 1:2 stoichiometry. The pale pink cobalt(II) complexes [Co(L1)2] (1), [Co(L2)2] (2) and [Co(L3)2] (3) were isolated as polycrystalline materials and characterized by elemental analysis and IR spectroscopy. In order to establish the molecular structures, single crystals suitable for X-ray crystallography have been obtained for complexes 1 and 2 by recrystallization from methanol and DMF solution, respectively. However, the investigations of the magnetic properties were performed on the dried, polycrystalline samples obtained from the reaction in ethanol solution.
3.2 Structural data
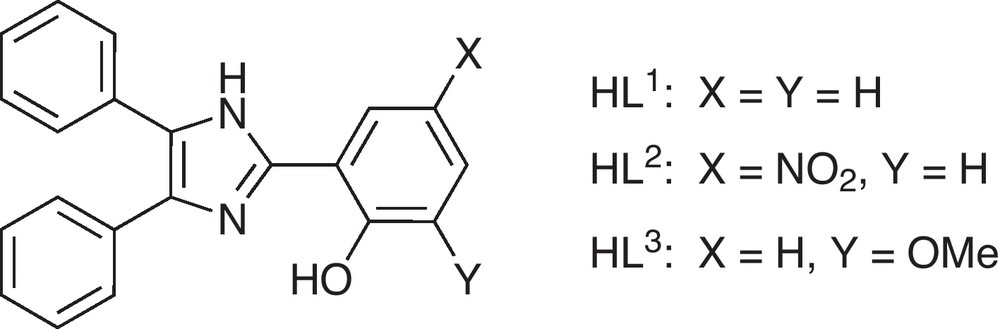
Complex 1 crystallizes in the monoclinic space group P21/c with two crystallographically independent complex molecules in the asymmetric unit. The molecular structure of one of the symmetry-independent molecules is depicted in Fig. 1 and selected bond lengths and angles are given in Table 2. In the crystal structure three additional co-crystallized methanol molecules per complex unit are present.
Molecular structure of one of the two symmetry-independent complex molecules [Co(L1)2] (1) in crystals of 1.3MeOH. Thermal ellipsoids are drawn at the 50% probability level. Hydrogen atoms are omitted for clarity.
Bond lengths (pm) and angles (°) at the cobalt(II) ions in complex [Co(L1)2] (1) for both symmetry-independent molecules in the crystals of 1.3MeOH.
| Con1–On1 | 193.3(3) | 192.0(3) |
| Con1–On2 | 192.1(3) | 192.4(3) |
| Con1–Nn1 | 197.3(3) | 197.2(3) |
| Con1–Nn3 | 197.6(3) | 196.7(3) |
| On1–Con1–On2 | 105.56(12) | 106.13(12) |
| On1–Con1–Nn1 | 93.86(12) | 94.51(13) |
| On1–Con1–Nn3 | 125.13(13) | 128.90(13) |
| On2–Con1–Nn1 | 132.17(13) | 123.74(13) |
| On2–Con1–Nn3 | 94.54(12) | 94.28(13) |
| Nn1–Con1–Nn3 | 109.31(13) | 112.24(14) |
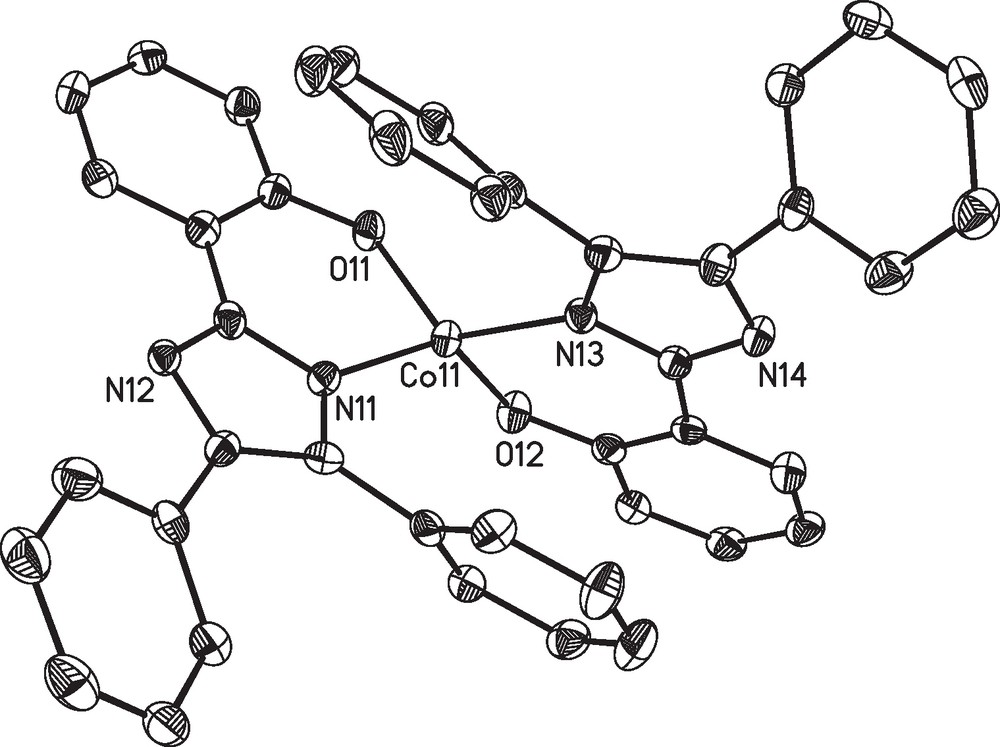
Complex 2 is found to crystalize together with additional co-crystallized DMF molecules in the monoclinic space group C2/c. The asymmetric unit contains only one complex molecule and the DMF molecules disordered over several crystallographic positions. The molecular structure of the complex molecule 2 is depicted in Fig. 2 and the corresponding bond lengths and angles around the cobalt(II) ion are listed in Table 3.
Molecular structure of the complex molecule [Co(L2)2] (2) in crystals of 2.2.5DMF. Thermal ellipsoids are drawn at the 50% probability level. Hydrogen atoms are omitted for clarity.
Bond lengths (pm) and angles (°) at the cobalt(II) ion in complex [Co(L2)2] (2).
| Co1–O1 | 191.3(2) |
| Co1–O4 | 191.4(2) |
| Co1–N1 | 197.6(2) |
| Co1–N4 | 197.1(2) |
| O1–Co1–O4 | 114.26(9) |
| O1–Co1–N1 | 94.39(9) |
| O1–Co1–N4 | 128.37(10) |
| O4–Co1–N1 | 124.62(10) |
| O4–Co1–N4 | 94.56(9) |
| N1–Co1–N4 | 103.32(10) |
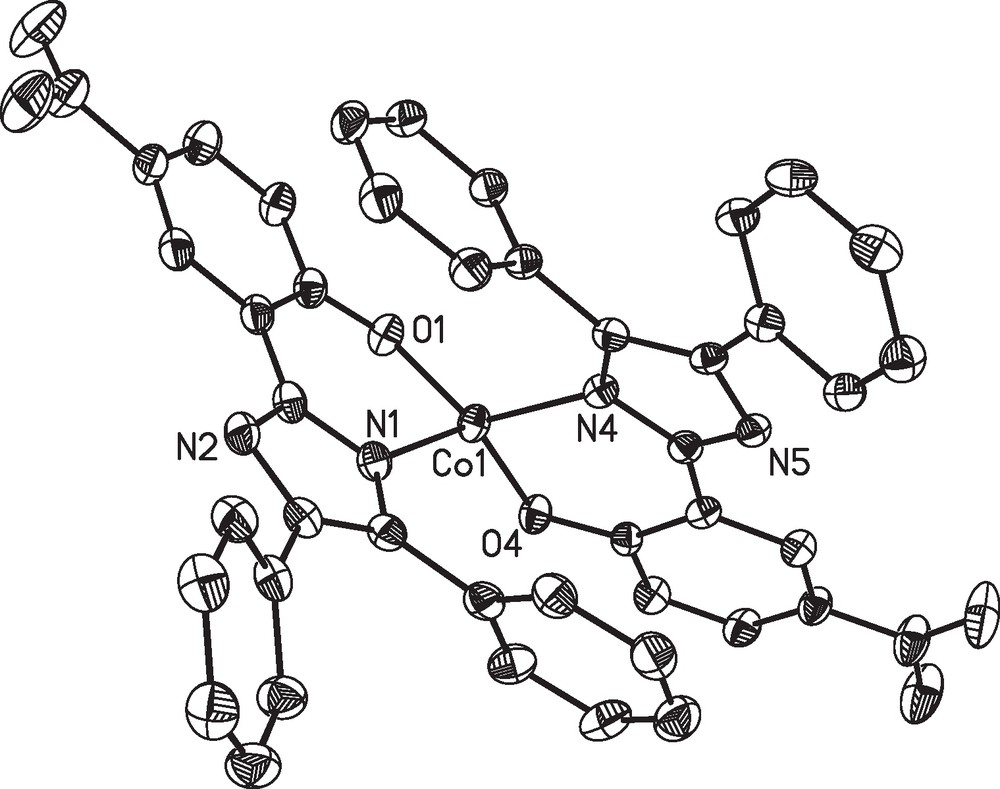
In both complexes the cobalt(II) ions are found in a distorted tetrahedral geometry. The coordination sphere is established by the phenolate oxygen atoms and the imidazol nitrogen atoms of two ligand fragments. The aromatic phenol and imidazole parts of each ligand are nearly coplanar (see Figs. 1 and 2). The coordination geometry of the cobalt centers of complexes 1 and 2 are very similar in both structures and, moreover, comparable to other examples with substituted 2-(1H-Imidazol-2-yl)phenol based ligands [46,47]. This particularly holds for the two symmetry-independent molecules of 1 found in the crystal structure, which correspond to the enantiomeric pair given by the chirality at the cobalt center. However, the crystal packing enforces deviations in the outer ligand sphere namely the aromatic rings (due to π-π and van der Waals interactions), as illustrated by an overly of the two independent molecules in Fig. 3. The average deviation of the positions of the atoms Con1, On1, Nn1, On2 and Nn3 (n = 1,2) used to fit the overlay of the two symmetry-independent molecules of 1 is only 11 pm.
Overlay of the two symmetry-independent complex molecules [Co(L1)2] (1) in crystals of 1.3MeOH. The structure of molecule 1 was inverted, the positions of the atoms Con1, On1, Nn1, On2 and Nn3 (n =1,2) were used to fit the overlay.
The angles between the two mean planes formed by the two ligand systems at the pseudotetrahedral cobalt centers of complexes 1 (72.6° and 75.8°) and 2 (74.9°) considerably deviate from the ideal 90° angle expected for a tetrahedral coordination geometry. An alternative approach for the related symmetry characterization of coordination polyhedra around metal ions is the so-called continuous shape measure [48,49], which gives a quantitative measure for the distortion of a given coordination sphere from tetrahedral and square planar by the corresponding shape measures, S(Td) and S(D4h). These values give a measure for the difference from ideal geometry, where zero indicates ideal geometry. Data is given in Table 4. For all three complex molecules of 1 and 2 these values indicate a distorted tetrahedral coordination geometry with the distortion about 1/4 of the full way between tetrahedral and square planar.
CSM parameters for the coordination geometries of the cobalt(II) ions in 1 and 2 (for notation see text).
| 1 (n = 1) | 1 (n = 2) | 2 | |
| S(Td) | 3.20 | 2.70 | 2.74 |
| S(D4h) | 19.20 | 20.90 | 20.59 |
| Φ(Td → D4h)a | 28% | 26% | 26% |
a Φ(Td → D4h) gives the angular fraction along the path from a tetrahedron to a square, for definition see Ref. [50].
The packing in the crystal structure of 1.3MeOH is primarily determined by hydrogen bonding interactions involving the phenolate oxygen (On1 and On2) and the protonated imidazole nitrogen atoms (Nn1 and Nn3) of the ligands and the co-crystallized methanol molecules. This leads to chains for both of the crystallographically independent molecules along the [001] direction with distances between the hydrogen-bonded heavy atoms in the range of 268–273 and 285–300 pm for O···O and N···O, respectively. Within the chains also π-π interactions between the aromatic rings of the ligands are observed. Finally, the aggregation of these chains is solely established via van der Waals interactions. This leads to Co–Co distances within the chains of about 790 pm and to interchain Co–Co distances larger than 946 pm.
In contrast to 1.3MeOH, the crystal structure of 2.2.5DMF exhibits hydrogen bonds only between the protonated nitrogen atoms N2 and N5 of the imidazole fragments of the coordinated ligands and the carbonyl groups of a co-crystallized DMF molecule, the latter showing a two-fold disorder. The observed N ⋯ O distances between the hydrogen bonded heavy atoms lie within the rang of 262 and 290 pm. The overall aggregation of the molecules in the crystal structure is solely given by van der Waals interactions, leading to intermolecular Co–Co distances larger than 849 pm.
3.3 Magnetic data
The molar magnetic susceptibilities of dried polycrystalline samples of complexes 1, 2, and 3 were measured in the temperature range from 300 to 2 K and applied static magnetic fields in the range of 1 to 5 kOe. Within this range no field dependence was observed. The variable temperature χT plots for 1–3 are depicted in Fig. 4. The experimental room temperature χT values of 2.75 emu K mol−1 for 1, 2.67 emu K mol−1 for 2, and 2.55 emu K mol−1 for 3 are significantly larger than the anticipated spin-only value for S = 3/2 of 1.87 emu K mol−1. However, these values are well within the range typically observed for highly anisotropic cobalt(II) ions with significant spin-orbit coupling [36–39]. Upon lowering the temperature the χT values only slightly decrease. Below about 100 K the χT values slowly show a significant decrease to values of about 1.7 to 2.0 emu K mol−1 at 2 K. The observed temperature profiles are characteristic for Curie-type behavior of noninteracting mononuclear cobalt(II) ions, where the decrease at low temperature is attributed to the anisotropy of the cobalt(II) ions rather than intermolecular antiferromagnetic interactions, which is consistent with the large Co–Co distances observed in the crystal packing of 1 and 2. The experimental χT data were analyzed using the spin Hamiltonian given in Eq. (2), which includes axial ZFS and Zeeman interactions:
| (2) |
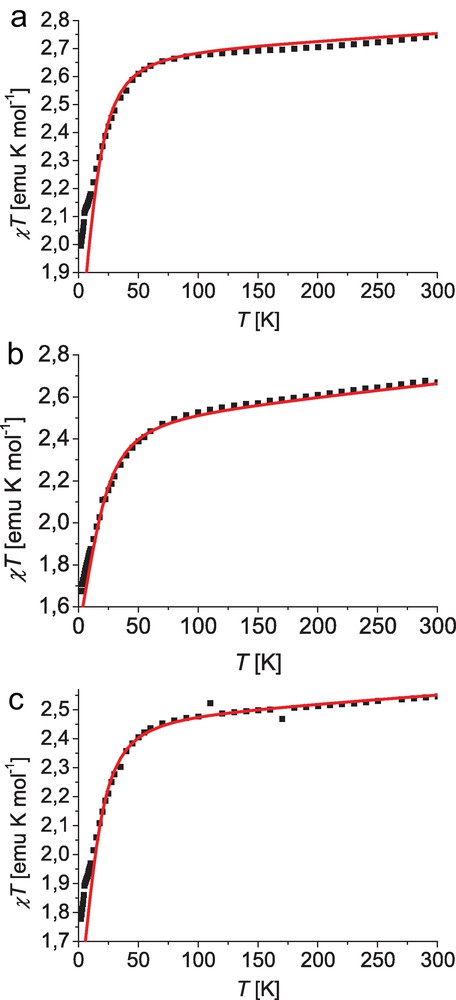
Plots for χT vs. T (black squares) and the best fit according to Eq. (2) (red lines) for complex 1 (top), 2 (middle), and 3 (bottom); applied magnetic field 2 kOe (for parameters see text).
The best fit including a correction term χTip for uncompensated temperature-independent magnetism results in g = 2.39, |D|=17 cm−1 and χTip = 2.9 × 10−4 emu mol−1 for complex 1, g = 2.30, |D| = 22 cm−1 and χTip = 6.0 × 10−4 emu mol−1 for complex 2, and g = 2.29, |D| =18 cm−1 and χTip = 2.9 × 10−4 emu mol−1 for complex 3. This leads to a good description of the experimental data in the temperature range from 300 to 15 K. Nevertheless, for temperatures below 15 K the predicted values are slightly smaller than those from experiment, which might be attributed to intermolecular interactions. However, the inclusion of an appropriate term in the Hamiltonian did not lead to a significant improvement of the fit. For this reason and to avoid overparametrization, effects from intermolecular interactions were not considered here. It should be noted, that it is difficult to determine the axial ZFS parameter D from magnetic susceptibility data derived from measurements on polycrystalline samples [51]. Besides the absolute value, this particularly holds for the sign of D which cannot unambiguously be determined on this basis, as the variations of χT are in general not very sensitive in this respect. However, a more sensitive probe in determining D values is the magnetization at intermediate fields and appropriate low temperatures, which is based on the deviation from the anticipated Brillouin behavior.
Variable-temperature magnetization measurements for complexes 1–3 were performed at fields ranging from 0 to 5 T and temperatures between 2 and 5 K (Figs. S1 and S2). The M vs. H data show an increase of the magnetization which becomes almost linear for higher fields without saturation to reach values of 2.13 μB for 1, 2.02 μB for 2, and 2.14 μB for 3 (at 2 K and 5 T). The observed lack of saturation together with the spreading of the curves in the M vs. H/T plots (Fig. S2) indicates the presence of a considerable ZFS in all three complexes. The fit on the M vs. H/T data was performed utilizing a full-matrix diagonalization approach [52] for the Hamiltonian given in Eq. (2) leading to D values of –41 cm−1 for 1 and –35 cm−1 for 2 and 3. For this fit the experimental data measured at 2 K was excluded, due to the obvious presence of additional low temperature effects like e.g. intermolecular interactions. This is clearly substantiated by comparing the chi-squared test parameters which are considerably smaller by almost one order of magnitude upon excluding the 2 K data set. Optimization for a positive sign of D in all cases does not converge to a reliable fit, indicating the right choice of sign. Not unexpectedly, the obtained absolute values deviate from the once derived from the susceptibility data, as the weighting in the magnetization based fit is clearly more emphasized on the relevant low temperature and high field data.
The SMM behavior of complexes 1–3 was investigated by frequency-dependent ac susceptibility measurements in the temperature range from 2 to 10 K. The in-phase (χ′) and out-of-phase (χ″) component of the ac susceptibility (χ = χ′ – iχ″) were measured using an alternating field of 3 Oe. Without an applied dc field no imaginary signal (χ″) could be observed for any of the compounds. For complex 2 even with an applied dc field only a marginal frequency dependence was observed for the in-phase component χ′ at temperatures below 5 K (Fig. S3). Moreover, as depicted in Fig. 5 only a very small out-of-phase signal χ″ was observed with no peak characteristic down to 2 K. For complex 1, however, the data depicted in Fig. 6 shows a clear out-of-phase signal below 8 K.
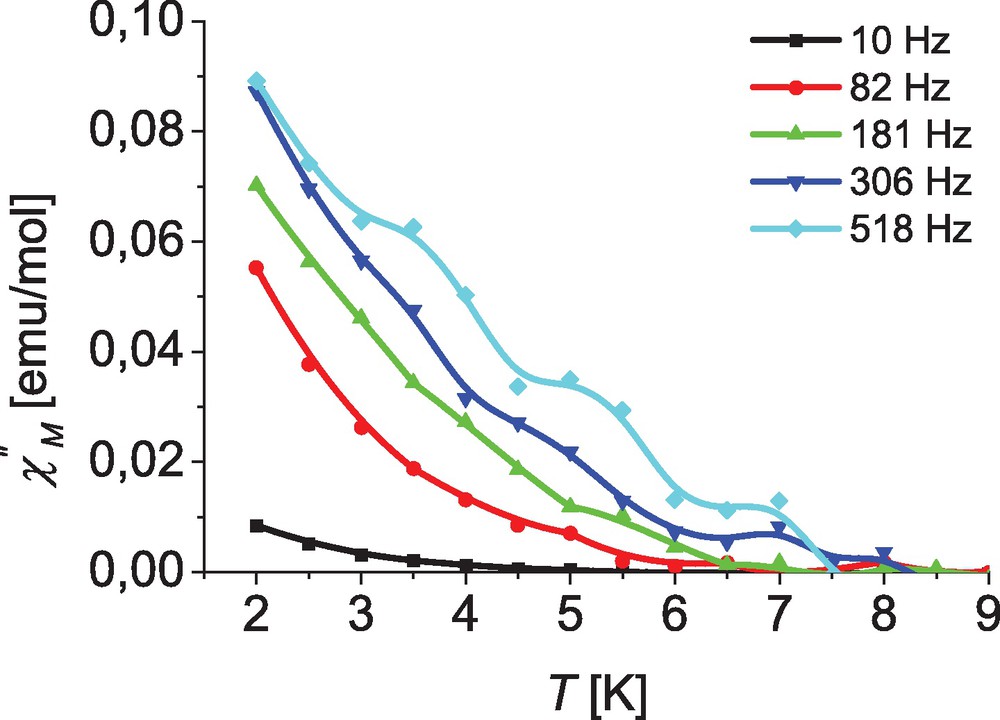
Temperature dependence of the out-of-phase ac susceptibility for complex [Co(L2)2] (2) at different frequencies with an applied field of 400 Oe; lines are guides for the eye.
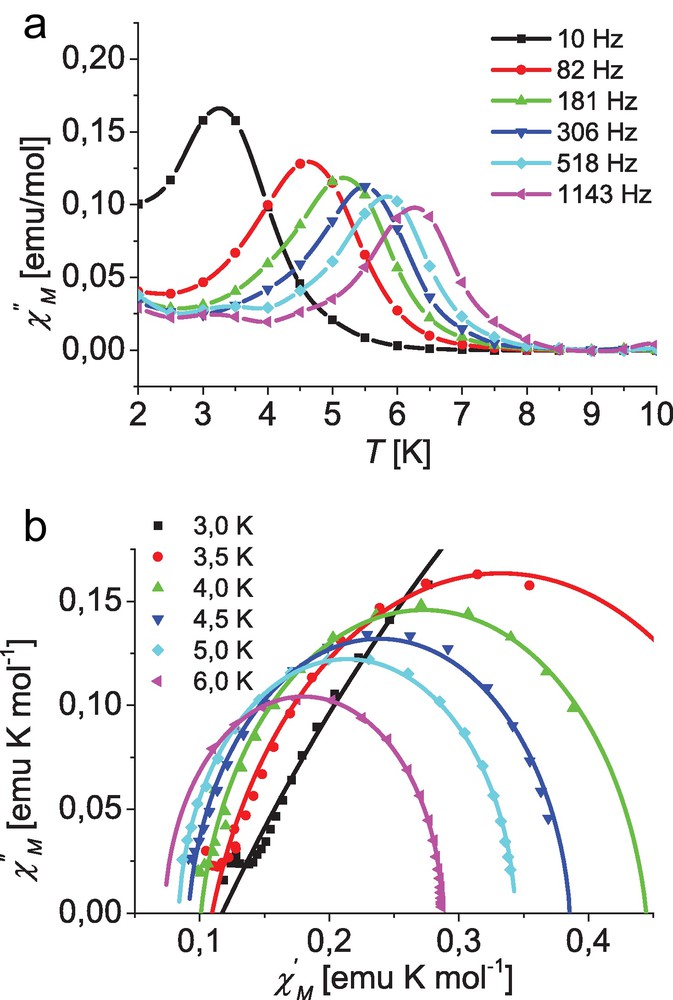
Top: Temperature dependence of the out-of-phase ac susceptibility for complex [Co(L1)2] (1) at different frequencies; lines are guides for the eye. Bottom: Cole–Cole plot for 1 at different temperatures with an applied dc field of 400 Oe; solid lines represent the best fit (for parameters see text).
The maximum for χ″ vs. temperature shifts from 3.5 K for 10 Hz to 6.5 K for 1143 Hz. Although a similar behavior is found for complex 3, clear defined maxima in temperature dependence of the out-of-phase signal χ″ are only observed for higher frequencies, as depicted in Fig. 7.

Top: Temperature dependence of the out-of-phase ac susceptibility for complex [Co(L3)2] (3) at different frequencies; lines are guides for the eye. Bottom: Cole–Cole plot for 3 at different temperatures with an applied dc field of 400 Oe; solid lines represent the best fit (for parameters see text).
The signals clearly deviate from the expected Lorentzian shape, with a considerable remaining intensity of χ″ at the low temperature side which indicates an additional relaxation process to be operative. At higher dc field (1000 Oe) the signal intensity of χ″ increases and the maxima become more pronounced. It seems that the additional relaxation process can be suppressed by higher dc fields.
Fitting the data of complexes 1 and 3 for each temperature to Eq. (1) leads to parameter sets including the adiabatic (χs for ω → 0) and isothermal susceptibility (χo for ω → ∞) as well as the magnetization relaxation time τc(T) and a which describes its width of distribution [53–55]. In the case of a paramagnetic compound obeying the Curie law the isothermal susceptibility, χo, represents the corresponding dc susceptibility. The obtained parameter sets can best be represented by a Cole–Cole plot as depicted in Figs. 6 and 7 for complexes 1 and 3, respectively. The simulations with the derived parameter sets are in excellent agreement with the experimental data particularly for higher temperatures at both applied dc fields (400 and 1000 Oe). However, in the case of low temperatures the measured data at high frequencies, representing data point at the very low end of the respective χ′ range, deviate from the simulated semicircle, again indicating a second relaxation process. Especially in the case of complex 1 this leads to a considerable uncertainty for the low temperature parameter sets at 2 and 2.5 K, as the number of available data points is insufficient for reliable fits. Therefore these data were not included in the corresponding fits and are not represented in the Cole–Cole plots depicted in the Fig. 6.
For the parameter α, representing the width of distribution of the magnetization relaxation times, a value close to 1 is expected for classical spin-glass systems (a = 1 means an infinitely wide distribution), whereas it will tend to 0 for a single relaxation time. In the case of 1 a decreases from 0.41 at 3.0 K to 0.014 at 6.5 K with an applied dc field of 400 Oe. With the higher dc field of 1000 Oe these values are even smaller, ranging from 0.19 at 3.5 K to 0.008 at 7.5 K.
In case of a classical thermally activated relaxation process [56], which takes place by excitation from a ground state Ms = ± 3/2 level to the higher energy Ms = ± 1/2 levels via the absorption of phonons from the lattice and de-excitation to the final state in which phonons are emitted, the anisotropic energy barrier Ueff can be determined from the Arrhenius law given in Eq. (3). For a graph of ln(τc) vs. 1/T this should result in a linear dependence for the high temperature regime of the relaxation from which Ueff and the attempt time τo can be extracted.
| (3) |
The corresponding Arrhenius plots for complexes 1 and 3 are depicted in Fig. 8.
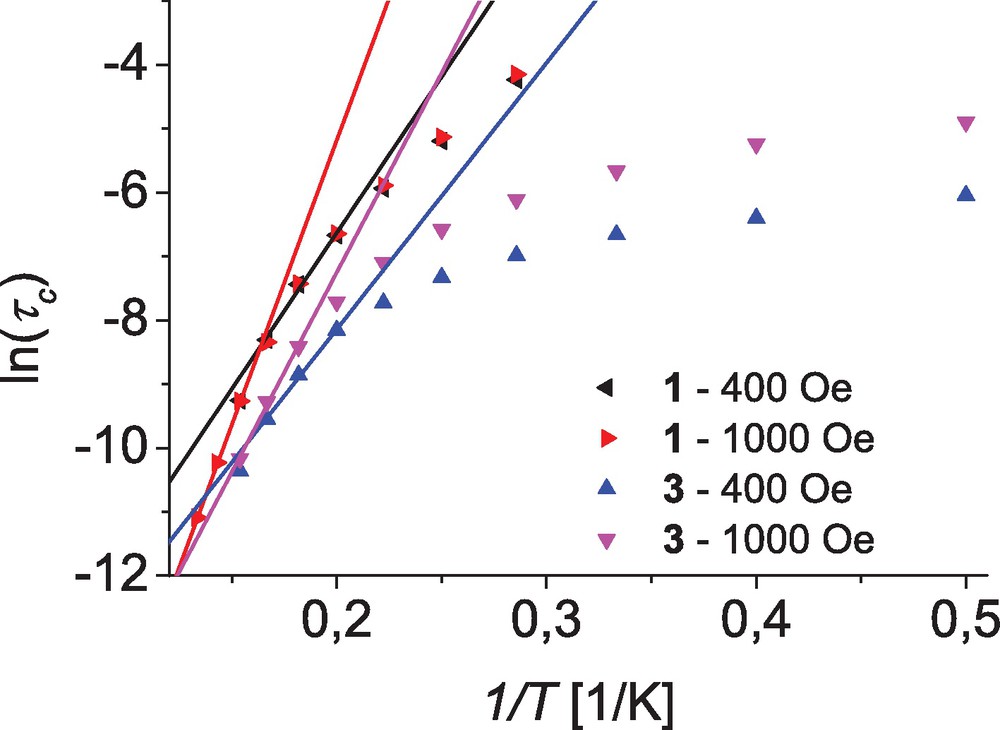
Arrhenius plots of relaxation times as ln(τc) vs. 1/T for the complexes 1 and 3; lines represent linear fits to the high-temperature data of measurements at dc fields of 400 and 1000 Oe (see text for details).
For complex 1 a clear temperature dependence for τc is observed with the high temperature data approaching the Arrhenius behavior expected for the thermally activated regime. This is independent from the applied dc field leading to an almost perfect overlay of the data obtained for both fields (400 and 1000 Oe). In contrast, for complex 3 a much more pronounced temperature dependence is observed for τc which, moreover, is different for the two applied dc fields. However, at higher temperatures these values approach each other, indicating a field-independent high temperature process. Whereas the low temperature data indicates a field-dependent relaxation process as expected form the χ″ behavior (vide supra). Unfortunately their is a considerable uncertainty in the determination of the τc values from Cole–Cole plots for data points at higher temperatures, as in these cases only the minor part of the corresponding semicircles are observed. Therefore only data up to a range of 6 to 7.5 K depending on the applied dc field were used in the fit to Eq. (3). For complex 1 this leads to Ueff = 49 K and τ0 = 7.5 × 10−8 s at an applied dc field of 400 Oe and for data points within the range of 5.0 to 6.0 K. Whereas for the higher dc field of 1000 Oe data from temperature range of 6.5 to 7.5 K could be used leading to Ueff = 89 K and τ0 = 1.0 × 10−10 s. In the case of complex 3 the fits lead to parameter sets of Ueff = 42 K and τ0 = 1.4 × 10−7 s for an applied dc field of 400 Oe (5.0 to 6.0 K) and Ueff = 63 K and τ0 = 2.6 × 10−9 s for 1000 Oe (5.5 to 6.5 K).
From these energy barriers (U = |D|(S2–1/4)) D values can be deduced for complexes 1 and 3 which range from 17 to 31 cm−1 and 15 to 22 cm−1, respectively. Even the upper limits of these estimated values, which correspond to the more reliable data sets measured at applied dc fields of 1000 Oe, are considerably smaller than those determined from the dc magnetization measurements. This however is not unexpected, as similar observations have been reported for tetrahedral cobalt(II) complexes in the literature [28,29], and may by explained by the presence of non-negligible QTM in these complexes.
4 Conclusion
We have synthesized a series of air-stable neutral mononuclear cobalt(II) complexes [Co(L)2] utilizing a sterically demanding bidentate ligand system which is base on the 2-(1H-imidazol-2-yl)phenol core fragment. This leads to a significantly distorted tetrahedral coordination geometry at the cobalt(II) ions. As a consequence a considerable spin-orbit coupling is observed for these complexes. The reported complexes appear to be the first examples of mononuclear tetrahedral cobalt(II) complexes with coordinated N,O ligands to exhibit slow magnetic relaxation. However, this SMM-like behavior is only observed under an applied static dc field. Future efforts will focus on the effects of structural and electronic tuning of the ligand system on the SMM-like behavior. Particular emphasis needs to be devoted to geometry and ligand field, in order to enhance the axial anisotropy in new complexes. This should allow for the design of examples with this N,O ligand system showing slow magnetic relaxation without applied static dc field.
Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (DFG) (PL 155/11-1 and PL 155/12-1) for generous funding of this project.


