1 Introduction
Important devices in computing, signal processing and communication technologies are based on bistable systems used as switches, memory elements and logic gates. Generally speaking, a system is bistable if it exhibits two stable output responses R for a single perturbation or input signal P, and shows a hysteresis loop in the curve R = f(P). Thus a bistable system reveals a different response for upward and downward sweeps of the input signal.
Two ingredients are required to generate a bistable phenomenon: (i) a feedback loop and (ii) a non-linear effect. In the particular case of optical bistability, – i.e. the bistability of the interaction of light with matter – the first experimental example of bistable set-up is a non-linear medium placed in a Fabry–Perot cavity [1]. It is important to note that the bistability is macroscopic in this kind of system, whereby the non-linearity is brought by the optical material and the feedback is produced by the cavity mirrors.
In the forthcoming decades, advances in nanosciences and nanotechnology promise to have major implications in materials devices and systems. For this reason, macroscopic properties such as optical bistability have to be scaled down to the nanometre level, in the domain of individual atoms, molecules or clusters. Recently, intrinsic (or mirrorless) optical bistability (IOB) of the emission from Yb3+ ion pairs have been observed in an ytterbium doped solid matrix [2]. However, the origin of this bistability remains puzzling, and different mechanisms are still debated.
For this reason, it is tempting to investigate the equivalent of IOB in magnetic resonance, reminding that concepts invented for nuclear magnetic resonance have often been a source of inspiration in optics community [3]. In the last decade, we showed that Electron Magnetic Resonance in solids is an intrinsically bistable phenomenon when several conditions are satisfied [4]. This effect is hereafter referred to as Bistable Electron Magnetic Resonance (BEMR). In this case, the non-linear effect is the saturation of the resonance, and the intrinsic feedback loop is provided by the nuclear spins via the Overhauser effect [5]. The detailed understanding of the mechanism of bistability allowed us to predict and observe BEMR in several systems, such as InP [6], metallic lithium colloids [7,8], gallium oxide [4], and to explain the origin of hysteresis observed in the EPR of GaAs–GaAlAs heterostructures [9]. It is important to realize that this elementary two-component elementary bistable system, composed of saturable absorbers (the electron spins) and intrinsic feedback elements (the nuclear polarization via the Overhauser effect) can in principle be extrapolated to UV-visible IOB with other types of two-component systems, such as atom pairs for example. In this case, the saturable absorber is the atom probed by the electromagnetic field, and the feedback system is the polarization induced on the second atom by the saturated absorption [10]. In this paper, we restrict IOB to BEMR, its magnetic equivalent.
2 The ‘shark-fin’ effect
The transition between two quantum states induced by an electromagnetic field, the basic event in spectroscopy, exhibits a symmetrical lineshape. Experimentally, the spectrum remains always unchanged upon upward and downward sweeps of the angular frequency ω of the electromagnetic field (or the magnetic field amplitude B0 at fixed frequency ω in the case of EPR). This usual situation is illustrated by the dotted line in Fig. 1b. However, it can be easily imagined that if the theoretical lineshape is bent in such a way that it describes a ‘shark-fin’ shape, the experimental spectrum becomes dependent on the field sweep direction, with a hysteresis width delimited by abrupt transitions at critical frequencies ω↑ and ω↓ (or magnetic field values B↑ and B↓ in EPR). This bistability window is characterized by a well-defined field range where the quantum system does not absorb the radiation for the increasing field sweep mode (the α-branch), while it strongly absorbs this radiation for the reverse field sweep mode (the γ-branch). In this case, a portion of the spectrum (the β-branch) cannot be recorded, and is lost experimentally (full line in Fig. 1b). It should be emphasized that this bistability in a two-state quantum system implies a memory of the field during the transition, since the response for given values of the control parameter (the frequency, or the magnetic field, etc.) depends on previous values of these parameters.

(a) Graphical representation of the response R of the system described by Eqs. (1) and (2). Case (i) corresponds to a monostable situation, while case (ii) corresponds to a bistable situation. (b) Shape of a transition induced in a two-state quantum system in monostable (case (i)) and bistable (case (ii)) situations. In the latter case, the transition exhibits a ‘shark-fin’ shape.
We have recently shown [10] that this ‘shark fin’ effect in a spectroscopic transition occurs if the quantum system is composed of two subsystems L and K, linked by a weak interaction V which fluctuates with a correlation time τc ≪ ℏ/V, the well-known ‘narrowing condition’ in magnetic resonance. The two subsystems retain the memory of their mutual interaction during τc. The consequence is that correlations between L and K vanish after a time t ≫ τc, which means that we may clearly distinguish the subsystem L probed by the electromagnetic field and the subsystem K responsible for the feedback loop. When the narrowing condition τc≪ ℏ/V is fulfilled, the steady-state response R (for example the absorption) of the LK system versus the angular frequency ω can be written with two coupled equations of the type [10]:
| (1) |
| (2) |
A renormalization of the resonance frequency is necessary to get a bistable ‘shark-fin’ shape. By renormalization, it is meant that the resonance frequency has to change continuously during the interaction with the electromagnetic field. This renormalization is included in Eq. (2), which directly comes from the condition τc≪ℏ/V [10]. Fig. 1a shows a graphical representation of the coupled Equations (1) and (2). The system is monostable (no memory) when the straight line (Eq. (2)) and the bell-shaped curve (Eq. (1)) have only one crossing point (case (i)). In this case, the resulting monostable lineshape, corresponding to the ensemble of crossing points versus ω, is represented by the dotted curve in Fig. 1b. The system is bistable when Eqs. (1) and (2) exhibit three crossing points α, β and γ (case (ii) in Fig. 1a). In this case, the response of the system, represented by the set of crossing points versus ω, exhibits the expected ‘shark-fin’ shape for bistability (full lines in Fig. 1b). Whether the response R is bistable or not depends only on the set of parameters a–e in Eqs. (1) and (2).
3 The mechanism of bistability in Electron Magnetic Resonance
We pointed out that a bistable shark-fin-like resonance might exist if two conditions are fulfilled: a non-linearity in the radiation-matter interaction, and a feedback mechanism. A collection of electrons in a magnetic field B0, characterized by a spin S = 1/2 interacting with neighbouring nuclear spins I via an hyperfine interaction A is the most elementary pair system that can exhibit a bistable interaction with a microwave electromagnetic field [4]. In this case, the non-linearity is the saturation of the resonance. It is well known that an electron spin resonance transition at energy ℏ ω = g β B0 is saturable at moderate value of the microwave field B1 if spin–orbit coupling effects are small, – i.e. if the g-factor is close to the free spin value ge = 2.0023. We thus consider the saturation factor s, defined as follows [11]:
| (3) |
| (4) |
| (5) |

Decomposition of the mechanism of BEMR into four elementary steps, for a system composed of electron spins interacting with nuclear spins via a hyperfine interaction A.
The feedback loop of BEMR is due to this polarization transfer, and must operate in such a way that it produces a renormalization of the resonance [10], – i.e. a shift of the resonance field (or frequency) during the interaction with the microwave radiation. This renormalization is possible only if the correlation time τc of the unpaired electron at the nuclear position is much shorter than ℏ/A [10]. For most paramagnetic defects in solids (impurities, point defects...), τc is generally characterized by τc > ℏ/A, so that the hyperfine interaction is resolved in the EPR spectrum, or contributes to the inhomogeneous broadening of the resonance line. Renormalization is thus not possible for localized electrons and large hyperfine coupling, and we do not expect bistability to occur in this case.
If the electron spin density is distributed over many nuclei, which occurs for shallow donors in semiconductors or for electrons delocalised in conduction band of solids, the hyperfine interaction A with each nuclear spin becomes small and ℏ/A is large. If, on the other hand, the spin density diffuses either by electron motion or by exchange interaction between electron spins, the correlation time τc of the unpaired electron at a nuclear site is considerably shortened (τc < 10−13s for exchange interaction in the meV range) and the condition τc≪ℏ/A prevails even for large hyperfine coupling A. The EPR line is exchanged (or motionally) narrowed with no remaining traces of the hyperfine splitting. It is important to note that in this case the electron resonance position is shifted by an effective nuclear field Bn = N A〈Iz0〉/g β, where N is the number of nuclei interacting with the electron spin, and the thermal equilibrium nuclear polarization is given by:
| (6) |
This nuclear field shifts the EPR resonance line to low field, and thus play the role of the feedback system as it modifies the saturation factor (4) via the effective field Beff = B0 + Bn seen by electron spins.
We have now to determine the equivalent of Eq. (2) for the feedback, s = f(Beff) and obtain the equation s = f(s) of bistability by combining this equation with Eq. (4). In the case of exchange or motional narrowing regime, the dynamic nuclear polarization occurs via the Overhauser effect. The decrease of the electron spin polarization 〈Sz〉 induced by saturation is transferred to 〈Iz〉 via the ‘flip-flop’ relaxation mechanism Δ(ms + mI) = 0 with a characteristic time Tx. This enhancement of the nuclear field Bn upon saturation is at the origin of the following feedback equation of bistability [4] (step 3 in Fig. 2):
| (7) |
| (8) |
| (9) |
| (10) |
As pointed out in the preceding part, bistability is expected when the line described by Eq. (7) has three crossing points with the curve of Eq. (4). This is equivalent to say that that the following equation s = f(s), obtained by combining Eqs. (4) and (7), representing step 4 in Fig. 2:
| (11) |
| (12) |
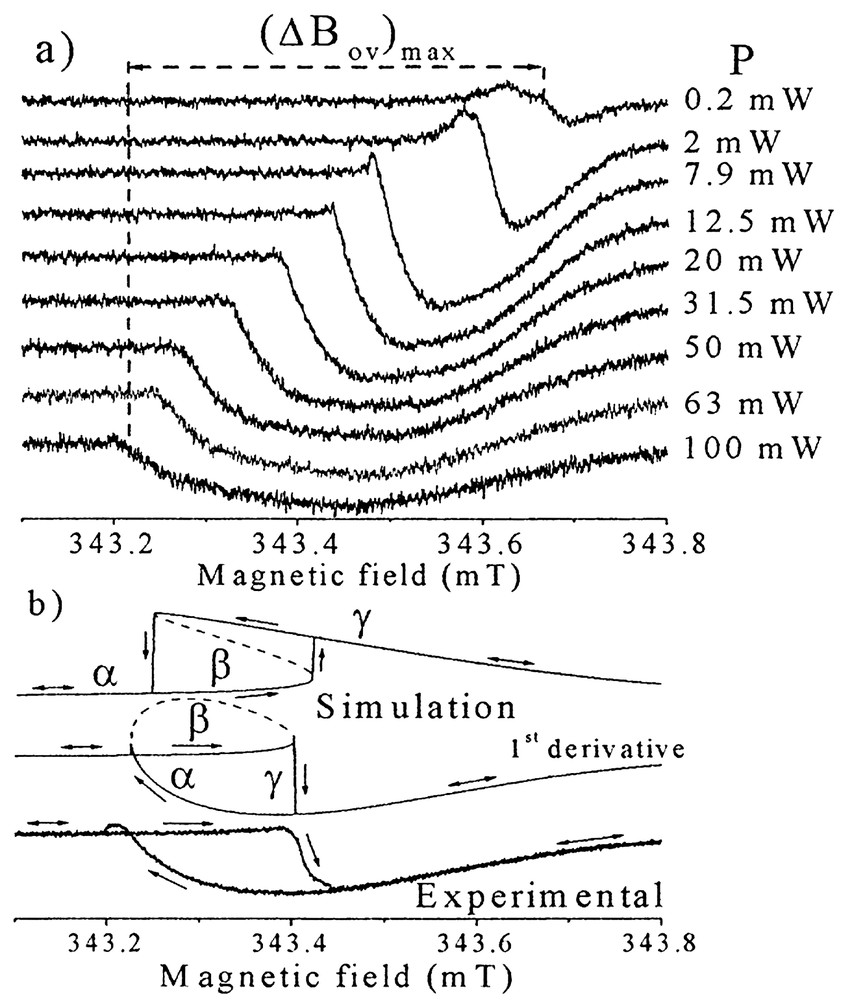
(a) EPR spectra of a β-Ga2O3 single crystal at 150 K, showing the renormalization of the resonance by the Overhauser effect, resulting from the narrowing condition τc≪ℏ/A. The spectra are recorded upon decreasing the magnetic field B0. (b) Selected BEMR spectrum at P = 63 mW. The simulation of the absorption and the first derivative of the absorption have been obtained with T1 = T2 = 1.4 × 10–7 s, (ΔBov)max = 0.47 mT and ℏ ω/g β = 343.51 mT.
4 Conditions for bistability
It should be emphasized that, in most cases, the EPR of shallow donors or conduction electrons in solids does not exhibit a bistable behaviour, although they correspond to the optimal condition of BEMR, as discussed in part 3. The reason is due to the fact that in most cases, Eqs. (4) and (7) have only one crossing point in all the magnetic field range. This implies that the values of the parameters B1, T1, T2 and (ΔBov)max in Eqs. (11) and (12) are such that the nuclear field Bn has only one value for each value of the external field B0. However, the analysis of BEMR in terms of non-linearity (saturable absorption, Eq. (4)) and feedback effect (Eq. (7)) allows us to predict the characteristics of compounds (chemical composition, electronic structure...) and the experimental conditions (temperature, magnetic field, microwave intensity) to obtain the ‘shark fin’ shape of BEMR. Equations (4) and (7) exhibit three crossing points in a given range of B0, the condition for bistability, when the slope of Eq. (7) is smaller than the tangent at the inflection point of the curve of Eq. (4). This condition gives [13]:
| (13) |
This inequality is controlled by two kinds of parameters: (i) external parameters represented by the temperature T and the microwave field B1, and (ii) material parameters represented by the electron relaxation times T1/T2, the nuclear spin I, the number N of nuclear spins interacting with each electron (the extension of the electronic wave function), the scalar hyperfine interaction A with each nucleus and the leakage factor f. In the case of a pure scalar (Fermi-type) hyperfine interaction, an estimation of N A in (13) is given by A0, the hyperfine interaction for a single ion or atom in a 2S spectroscopic state, – i.e. a single electron in a s-atomic orbital. We thus expect N A f ≤ A0. As B1 is a control parameter, the right-hand member of Eq. (13) can be minimized with respect to B1, which gives:
| (14) |
This critical inequality expresses the condition for the existence of at least one value of the microwave field B1 for which BEMR can be observed. By using Eq. (8) and the expression of the peak-to-peak linewidth of the unsaturated line, this inequality can be simplified into a more general form for the existence of bistability:
| (15) |
The bistability condition (14) contains all the structural information concerning potential candidates for BEMR. The most favourable compounds should be characterized by long T2, high nuclear spin, strong hyperfine interaction and a leakage factor close to one. Transverse relaxation time T2 is related to both the electronic structure of the conduction band edge and structural defects (impurities, intrinsic defects...). In the situation of extreme narrowing regime, imposed by the condition τc≪ℏ/A, the electron relaxation times of electrons in (or close to) the conduction band edge are given by [14]:
| (16) |

Influence of the electron relaxation time T2 on the BEMR shape. Parameters of the calculation: I (I + 1) N A f = 13 650 MHz (corresponding to gallium nuclei), T = 150 K, B1 = 6 × 10–2 mT, and T1 = T2.
The other important factor for bistability in condition (14) is the term I (I + 1) N A f, which determines the intensity of the nuclear polarization at a given temperature and external magnetic field. For a solid containing one type of nuclear spins, this term is written as [15]:
| (17) |
The particularly favourable characteristics of β-Ga2O3, namely shallow donors in exchange interaction, gallium nuclei with I = 3/2, strongly anisotropic band structure, conduction band edge made of 4s gallium orbitals, explain why this compound exhibits BEMR up to room temperature [15]. However, from known values of T2 and hyperfine coupling for the semiconductor InP and for metallic lithium particles embedded in insulating matrices, we expect BEMR at liquid helium temperature and X-band frequency with these compounds. For example, Fig. 5 shows the calculated EPR spectrum of submicronic metallic particles at different microwave power values. Fig. 6 shows the experimental spectrum of lithium particles produced by UV irradiation of LiH powder [8]. The spectrum is simulated by summing the contributions of two types of lithium, one with a long T2 (population A, T2 = 4.8 × 10–6 s) and the other with a shorter T2 (population B, T2 = 9 × 10–7 s). The BEMR spectrum of shallow donors in InP single crystal at 3 K is shown in Fig. 7, where it is compared with the spectrum predicted by considering only parameters known in the literature [6].

Theoretical EPR spectrum for submicronic metallic lithium particles. Parameters of the calculation: T = 4 K ; T1 = T2 = 0.5 × 10–6 s; I (I + 1 ) N A f = 200 MHz.

Experimental and calculated BEMR spectra for submicronic lithium particles at 4 K produced by UV irradiation of LiH powder. Parameters of the calculation : P = 25 mW. Two populations of particles are considered. Population A: T1 = T2 = 5 × 10–6 s; I (I + 1) N A f = 110 MHz. Population B: T1 = T2 = 9×10–7 s ; I (I + 1) N A f = 140 MHz.

Experimental and calculated BEMR spectra for InP at 3 K. Parameters of the calculation: P = 5 mW (B1 = 10–2 mT), T1 = T2 = 4 × 10–8 s, I (I + 1) N A f = 168 430 MHz. The unsaturated spectrum (P=0.1 mW, B1 = 1.6 × 10–3 mT) is shown on the top of the figure.
5 Analogy with other types of bistability: the dynamic potential
Bistable systems in physics, chemistry and biology are often described by a potential U = f(Q) where Q is a configuration (or reaction) coordinate, as shown in Fig. 8 [16]. The minima Uα and Uγ represent the stable steady states, while the local maximum Uβ is the unstable steady state. The shape of the potential is determined by the control parameters, so that the hysteresis cycle across a bistable resonance (Fig. 1b) can be described as follows in the potential representation, in terms of the overdamped motion of a fictitious particle in the Q space. Starting from the low frequency ω (or low-field B0) and sweeping up to ω ≤ ω↓, the potential is monostable (Fig. 8a). For ω↓ < ω < ω↑, the branch α of the spectrum of Fig. 1b is recorded, which corresponds to the bistable potential of Fig. 8b, with the system trapped in the α-state. For ω = ω↑, the spectrum exhibits an abrupt increase of intensity (Fig. 1b), which corresponds to a vanishing potential barrier in Fig. 8c, with the system making a transition to the γ-state. The system becomes monostable for ω > ω↑ (γ-state only). For a decreasing variation of ω, and starting from ω > ω↑, the spectrum of Fig. 1b follows the γ-branch up to ω > ω↓, which again corresponds to the potential of Fig. 8b, but the system is now trapped in the γ-state. The abrupt variation of intensity at ω = ω↓ in Fig. 1b corresponds to the potential of Fig. 8d, with a vanishing potential barrier and a transition to the stable α-state.
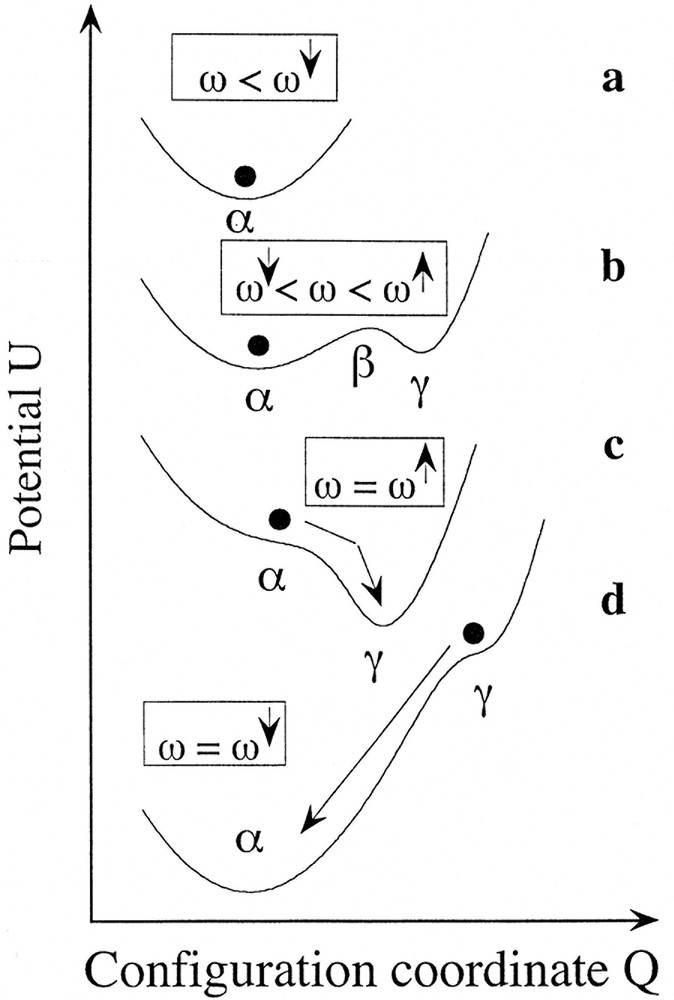
Representation of the dynamic potential U versus configuration coordinate Q, for four selected situations of the bistable transition of Fig. 1b (case ii).
In order to get a more familiar picture of BEMR in terms of overdamped motion in the potential U = f(Q), let us consider the rate equation for the dynamic nuclear polarization [17]:
| (18) |
This equation describes the time evolution of the nuclear field Bn. The steady-state nuclear field, corresponding to ∂Bn/∂t = 0 in Eq. (18), is reached after a period in the order of magnitude of the electron-nuclear (flip-flop) relaxation time Tx, which amounts to 0.1 to 0.5 s in β-Ga2O3 at 150 K [17] and 140 s in InP at 3 K [6]. Equation (18) being autonomous and a continuous function of a single variable (Bn), it is similar to the equation of overdamped motion of a fictitious particle in the magnetic field space, for which we may associate the potential U, defined as follows:
| (19) |
| (20) |
This potential exhibits two minima (bistability) if condition (13) is satisfied. Comparison of Eqs. (20) and (12) shows that the steady state BEMR intensity is proportional to the second derivative of the potential at the minima α and γ, [U″ (Bn)]α ,γ=(∂2U/∂Bn2)α ,γ:
| (21) |
Fig. 9 shows a 3D plot of the dynamic potential calculated from Eq. (20) for InP, corresponding to the spectrum of Fig. 7. Under slow sweeping of the magnetic field B0, the shape of the potential is continuously modified, and exhibits either one or two minima. The ‘trajectory’ of the polarized electron-nuclear spin system (the fictitious particle) in the potential is marked by the full line in Fig. 9. It can be seen that the system switches from one potential minimum to the other when the potential barrier vanishes. Fig. 9 also shows that the shape of the first derivative of the EPR absorption is proportional to the second derivative of the dynamic potential.

(a) 3D plot of the dynamic potential calculated from Eq. (20) for InP at 3 K, corresponding to the spectrum of Fig. 7. (b) Variation of the BEMR intensity (Eq. (21)) deduced from the trajectory of the fictitious particle (the resonating electron–nuclear-spin system) in the potential.
6 Conclusion
Magnetic resonance in an electron spin system under extreme narrowing condition is an intrinsically bistable resonance when the solid contains nuclear spins. BEMR implies a memory effect at the level of elementary quantum systems interacting with an electromagnetic field. Despite its originality with respect to other bistable systems described at the molecular level, such as bistable spin transitions for example [18], the similarity of these types of bistability appears more clearly when BEMR is described in terms of dynamic potential in the nuclear field space. BEMR also provides the simplest case of ‘optical’ bistability in a pair system AB, where the saturable absorber A is the electron-spin system and the feedback system B is the ensemble of nuclear spins polarized by A. The mechanism of BEMR can be extrapolated to IOB in pair systems AB, including atomic pairs [10].


