Stoichiometry of uranyl hydrolysis reaction in acidic aqueous solutions from the evidence of oxygen exchange kinetics

Leonid G. Mashirov; Vladimir A. Mikhalev; Dmitry N. Suglobov

doi:10.1016/j.crci.2004.06.005

Résumés

Anglais
Français

The kinetics of uranyl oxygen exchange with water molecules in aqueous solutions was studied in the pH range 1–4 and uranium concentration range 10^–4–0.1 M. It was confirmed that the exchange is stimulated by hydrolyzed uranyl species. From the evidence of data on the kinetics of uranyl oxygen exchange the reaction stoichiometry of uranyl hydrolysis was determined. The scheme of uranyl hydrolysis involving formation of ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ , ${({UO}_{2})}_{2} {(OH)}_{3}^{+}$ , and other hydrolyzed species was proposed.

Étude de l'hydrolyse de l'uranium hexavalent en milieu acide par échange isotopique de l'oxygène. L'échange isotopique de l'oxygène de l'ion uranyle avec les molécules d'eau a été étudié dans le domaine de pH de 1 à 4 et de concentration en uranium de 10^–4 à 0,1 M. Cet échange a lieu par l'intermédiaire d'espèces hydrolysées de U(VI). La stoechiométrie des formes hydrolysées de U(VI) est déduite des vitesses d'échange isotopique. En particulier, les espèces ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ et ${({UO}_{2})}_{2} {(OH)}_{3}^{+}$ ont été clairement identifiées. Un schéma d'hydrolyse est proposé.

1 Introduction

Uranyl hydrolysis is one of the most important processes in uranium chemistry and geochemistry. It is actively studied since the Manhattan Project, and uranyl hydrolysis and, especially, hydroxo-carbonate and hydroxo-silicate complex formation are now of particular interest in view of radioactive waste management problems. The pH-metry is the main source of information about uranyl hydrolysis. The hydrolysis mechanism is traditionally derived from the titration curves of a uranyl salt solution with an alkali, using the stoichiometry and corresponding stability constants of uranyl hydroxo complexes as parameters. The set of these parameters differed from one work to the other [1–5].

The results were summarized by Baes and Mesmer [6], Fuger [7], and Fuger and co-workers [8] (see also the Medusa software: www.Kemi.kth.se/inorg/medusa), and the following formal equilibriums in acidic aqueous solutions were proposed:

{UO}_{2}^{2 +} + H_{2} O = {UO}_{2} {OH}^{+} + H^{+}

(1)

{2 UO}_{2}^{2 +} + H_{2} O = ({UO}_{2})_{2} {OH}^{3 +} + H^{+}

(2)

2 {UO}_{2}^{2 +} + 2 H_{2} O = {({UO}_{2})}_{2} {(OH)}_{2}^{2 +} + 2 H^{+}

(3)

3 {UO}_{2}^{2 +} + 5 H_{2} O = ({{UO}_{2})}_{3} {(OH)}_{5}^{+} + 5 H^{+}

(4)

However, it is not evident that all of these equilibriums be realized.

In recent years, various structural, mainly spectroscopic methods [9–12] were used in studying uranyl hydrolysis, but the results were interpreted with attraction of pH-metric data, and, therefore, the uncertainty in determination of the composition of hydrolyzed uranyl species, characteristic of pH-metry, was kept.

In this work, information about the composition of hydrolyzed uranyl species was derived from data on the kinetics of uranyl oxygen exchange in aqueous solutions, which is a catalytic reaction. At present only one direct catalyst of oxygen exchange, namely uranyl(V) ion, is well known [13,14], and it is assumed that the second catalyst of oxygen exchange is hydrolyzed uranyl [15].

We found that the rate of oxygen exchange is negligible in acidic medium (at acid concentration above 0.2 M) and monotonically increases with increasing pH according to the equation:

d C / d t = k [{(U O_{2})}_{n} {(OH)}_{m}] = k K {[{U O_{2}}^{2 +}]}^{n} {[H^{+}]}^{- m}

(5)

where k is the rate constant of oxygen exchange and K is the equilibrium constant of the hydrolysis reaction:

n {U O_{2}}^{2 +} + m H_{2} O = {({UO}_{2})}_{n} {(OH)}_{m}^{(2 n - m) +} + m H^{+}

(6)

n and m being the reaction orders with respect to the reactants, and, at the same time, the stoichiometric coefficients of the hydrolysis reaction, which can be considered as a simple reaction.

Therefore, when dissolving in water a uranyl salt, labeled with oxygen-18 in the uranyl group, we can monitor the rate of oxygen-18 elimination from the uranyl group depending on concentrations of uranyl and hydrogen ions. From these data, we can directly determine the reaction orders of the hydrolysis with respect to the reactants, independently on pH-metric data, and, hence, find the stoichiometric coefficients of the hydrolysis reaction.

2 Experimental

The experiments aiming at determining the oxygen exchange rate were carried out as follows [16]. A sample of crystalline cesium uranyl trinitrate containing 50–70% oxygen-18 in the uranyl group was dissolved in a fixed volume of water with natural content of ¹⁸O at a known initial pH value. If required, the solution pH was adjusted with dilute nitric acid, and than the solution was allowed to stay at a fixed temperature for a definite time. Then an aliquot of the solution was introduced into the mixture of acetic acid and sodium acetate, where the uranyl oxygen exchange immediately stopped, and poorly soluble sodium uranyl triacetate NaUO₂(CH₃COO)₃ was precipitated. The latter was separated from the solution, washed with ethanol, dried in a vacuum, and introduced into the potassium bromide pellet, and the IR spectrum was recorded over the range 650–960 cm^–1. In this region, the antisymmetric stretching vibrations of three uranyl isotopic forms ¹⁶OU¹⁶O^2+,¹⁶OU¹⁸O²⁺, ¹⁸OU¹⁸O²⁺ at 932, 916, and 886 cm^–1, respectively, acetate skeleton vibration δ(COO) at 678 cm^–1, and several weak absorption bands, among them ν_s ¹⁶OU¹⁸O at 826 cm^–1, were observed (Fig. 1). The integral intensities of uranyl isotopic forms allow calculation of concentration of isotopic forms as a function of time at various temperatures and concentrations of uranium and hydrogen ions and determination of the rate of uranyl oxygen-18 loss as the rate of uranyl exchange. Since the uranyl oxygen-18-to-oxygen-16 ratio in the system is small, we can neglect the reverse transfer of oxygen-18 from the water bulk to uranyl.

Fig. 1
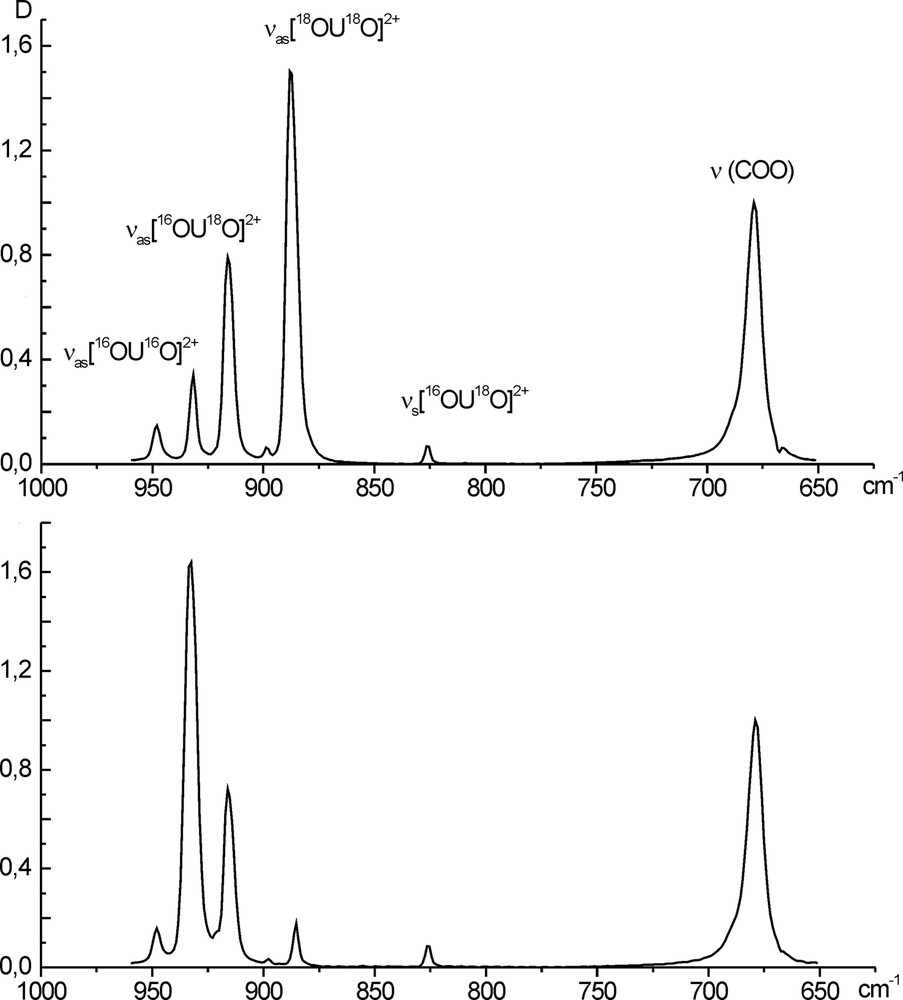
IR spectra of NaUO₂(CH₃COO)₃ in KBr pellets (a) precipitated from the initial solution, 70% ¹⁸O and (b) precipitated from the solution kept for a certain time.

In the experiments, the uranium concentration was varied from 10^–4 to 10^–1 M, pH, from 1 to pH of hydroxide precipitate formation (3.48 for 0.1 M and 5.6 for 0.001 M uranium solutions), storage time of solutions, from 0.5 to 10³ h, and temperature, from 1 to 60 °C. The main error in determination of t_1/2 was governed by the error in pH measurements, which was 0.02 units.

3 Results and discussion

The suitable form of presentation of kinetic data is the dependence of the half-exchange time t_1/2 on the concentration of reactants (uranyl concentration and pH). In this case, according to the Noyes–Ostwald formula [17]

\log t_{1 / 2} = - (n - 1) \log C_{U} + m pH + const

The results on the kinetics of uranyl oxygen exchange are presented in Fig. 2 as a family of dependences of logarithm of the half-exchange time on the solution pH at fixed uranium concentrations. Two groups of the curves were obtained at 28.7 and 15 °C. The first group corresponds to low pH values and describes initial stages of hydrolysis. In the first group, the dependences are well-fitted by straight lines with the slope close to –2 for uranium concentrations 0.003, 0.01, and 0.03 M, which corresponds to the reaction order with respect to hydrogen ion –m = –2. For higher uranyl concentrations, 0.05 and 0.1 M, m increases to 2.4 and 2.7, respectively (Table 1).

Fig. 2
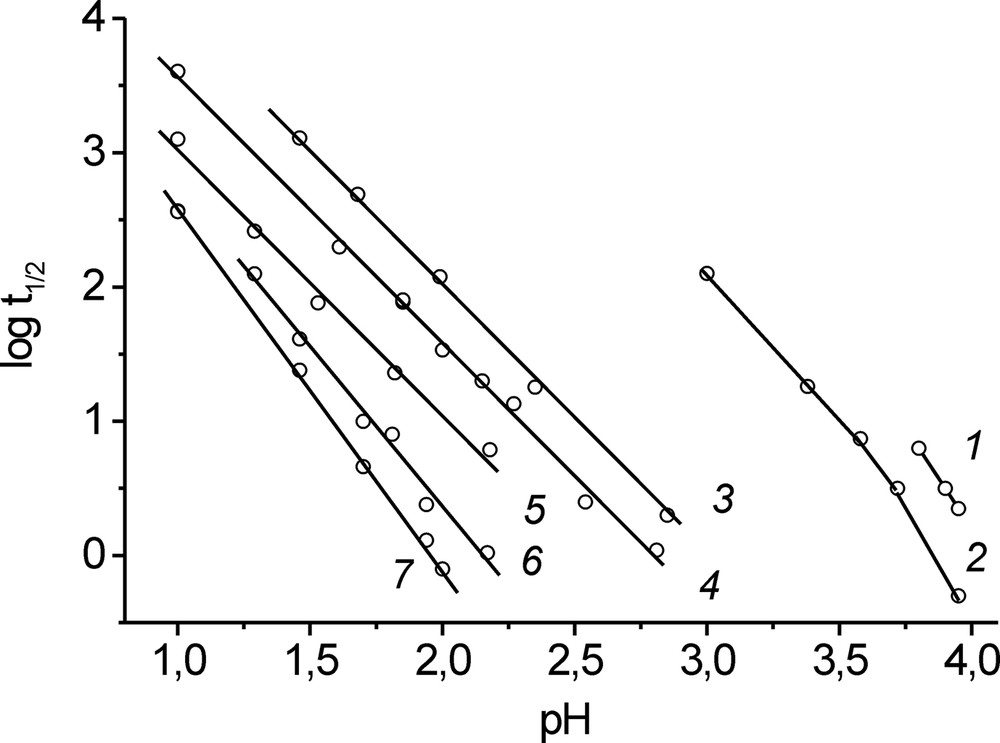
Half time of oxygen exchange as a function of pH. Uranium concentration (M): (1) 10^–4, (2) 5 × 10^–4, (3) 0.003, (4) 0.01, (5) 0.03, (6) 0.05, and (7) 0.1. Temperature: (**1, 2**) 15 °C and (**3–7**) 28.7 °C.

C_U (M)	T (°C)	pH range	m
0.0001	15	3.80-3.95	2.90
0.0005	15	3.00-3.58	2.08
0.0005	15	3.58-3.72	2.55
0.0005	15	3.72-3.95	3.45
0.003	28.7	1.46–2.85	2.04 ± 0.036
0.01	28.7	1.00–3.81	1.95 ± 0.10
0.03	28.7	1.00–2.18	1.98 ± 0.045
0.05	28.7	1.29–2.17	2.38 ± 0.13
0.1	28.7	1.00–1.94	2.65 ± 0.036

Vertical cross-sections of the above plots give the dependences of log t_1/2 on uranium concentration at fixed pH values. Each of these dependences can be fitted by two linear parts with a break at C_U = 0.03 M (Fig. 3). The slopes of the first part (C_U in the range 0.003–0.03 M) are the same, being equal to –1, which, in accordance to the Noyes–Ostwald equation, corresponds to the hydrolysis reaction order with respect to uranium n = +2. The slopes of the second part (C_U in the range 0.03–0.1 M) increase with increasing pH and correspond to the reaction orders with respect to uranium n = 2.2, 2.6, and 3.4 at pH 1.2, 2.0, and 2.5, respectively (Table 2).

Fig. 3
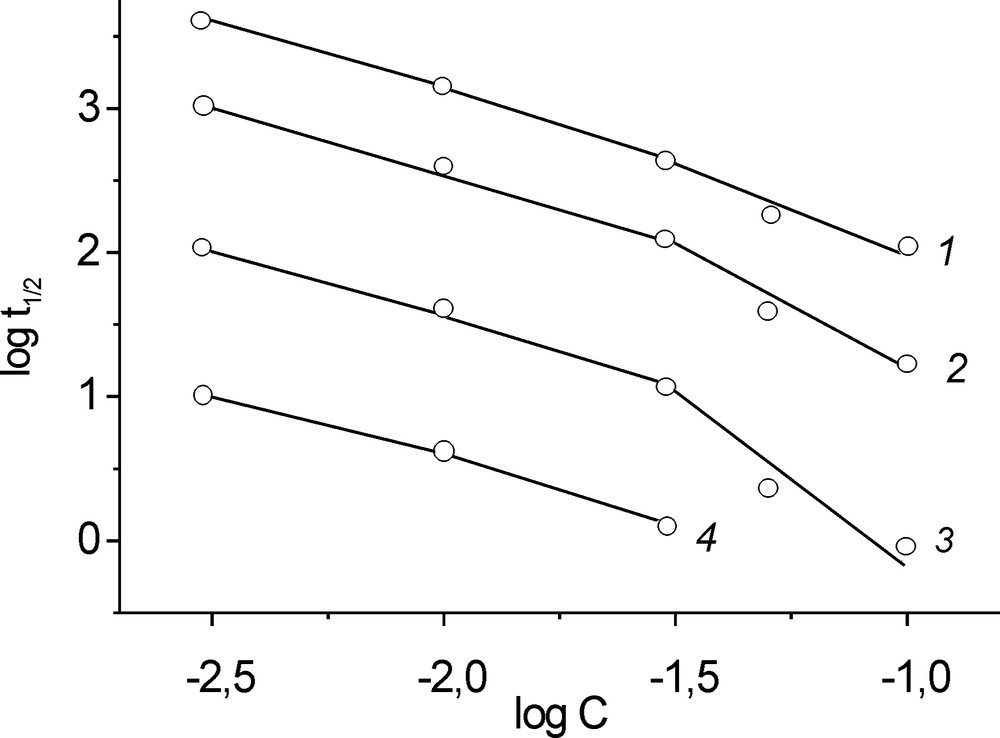
Half time of oxygen exchange as a function of uranium concentration. pH: (1) 1.20, (2) 1.50, (3) 2.00, (40) 2.50. Temperature: 28.7 °C.

pH	T (°C)	C_U range	n
1.20	28.7	0.003–0.03	1.99 ± 0.05
0.03–0.1	2.20 ± 0.09
1.50	28.7	0.003–0.03	2.00 ± 0.05
0.03–0.1	2.40 ± 0.19
2.00	28.7	0.003–0.03	1.99 ± 0.05
0.03–0.1	3.20 ± 0.20
2.50	28.7	0.003–0.03	1.96 ± 0.04

The number of experiments performed at 15 °C (C_U 10^–4 and 5 × 10^–4 M) is significantly lower (they correspond to the pH range close to the beginning of uranyl-hydroxide precipitation). Nevertheless, the results obtained are adequate to reveal the tendencies in variation of the reaction orders with respect to the reaction components. In the pH range 3.0–3.2, the m value is equal to 2 and with further increase in the pH the reaction order n increases to 2.6 in the pH range 3.58–3.72 and to 3.5 in the pH range 3.72–3.95 (Fig. 2, curve 2). In this pH range, the reaction order with respect to uranium, estimated from the differences between the points at curves 1 and 2, is close to 2 (Fig. 2).

In the course of the experiments, we measured t_1/2 at various temperatures, which allows evaluation of the activation energy of oxygen exchange. The results are given in Fig. 4 as a plot log k−1000/T. In the C_U range 0.003–0.03-M and pH domain 1–3, the activation energy E^# is 122 ± 5 kJ mol^–1, and in the C_U range 0.005–0.03-M, at pH 3.4, E^# = 42.8 ± 3.6 kJ mol^–1.

Fig. 4
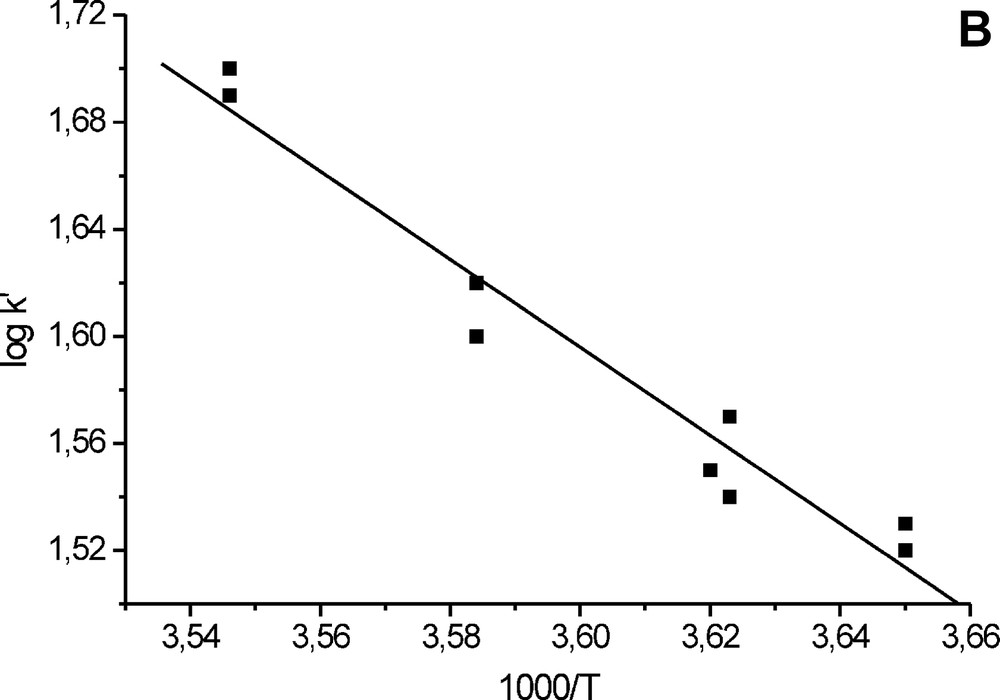
Rate constant of oxygen exchange as a function of temperature. (a) C_U 0.005–0.03 M, pH 1–3; (b) C_U 0.005–0.03 M, pH 3.4.

The results obtained allow the following interpretation of the exchange experiments. In dilute solutions (C_U in the range 0.0001–0.03 M) with a low pH, where n = 2 and m = 2, the uranyl hydrolysis can be presented by Equation (3), in which two uranyl ions and two hydroxyl ions form the ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ complex. From the reaction stoichiometry, it follows that the necessary condition for uranyl hydrolysis is the close contact of two hydrated uranyl ions. This results in abstraction of protons from coordinated water molecules in the field of two uranyl ions with formation of the ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ complex, having a cyclic structure with bridging hydroxyls. This is supported by the fact that the sum of energies of two bridging bonds involving monoatomic ligands is greater than the energy of one terminal bond (see, e.g., [18]). The reaction proceeds through formation of intermediates with substantially weakened axial uranium–oxygen bond, in which the oxygen exchange occurs.

At pH above 3, the predominant process is the spontaneous hydrolysis of 2:2 species:

{(U O_{2})}_{2} {(OH)}_{2}^{2 +} + H_{2} O = {(U O_{2})}_{2} {(OH)}_{3}^{+} + H^{+}

and of 2:3 species

{(U O_{2})}_{2} {(OH)}_{3}^{+} + H_{2} O = {(U O_{2})}_{2} {(OH)}_{4} + H^{+}

with subsequent coagulation of neutral (UO₂)₂(OH)₄. This follows from the increase in the reaction order with respect to hydroxyl ion in the solutions with pH higher than 3 at a constant reaction order with respect to uranium equal to 2.

The mechanism proposed is supported by an abrupt decrease in the activation energy of oxygen exchange from 122 kJ mol^–1 over the pH range 1–3 to 42.8 kJ mol^–1 at pH 3.4 and by the change in the nature of the uranyl oxygen exchange. At pH < 3, the exchange proceeds independently for each oxygen atom of the uranyl group and, at pH > 3.0, the contribution of simultaneous oxygen exchange rapidly grows from 25% at pH 3.7 to 80% at pH 3.9 [16].

Within the uranium concentration range 0.03–0.1 M and pH domain 1–3, the slopes of straight lines in Fig. 2 increase so much that the reaction orders with respect to both uranium and hydrogen ion increase (Tables 1 and 2). We explain this fact by the formation of cyclic trimers ${({UO}_{2})}_{3} {(OH)}_{3}^{3 +}$ at higher uranium concentrations. Then, by the analogy with dimer ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ , formation of 3:4, 3:5, and 3:6 hydroxo complexes can be assumed at pH > 3.

The results obtained give the following pattern of uranyl hydrolysis in acidic aqueous solutions (Fig. 5). The only ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ complex dominates in the wide range of uranium concentration from 10^–4 to 0.03 M and pH from 1 to 3. Higher oligomers with the composition ${({UO}_{2})}_{3} {(OH)}_{3}^{3 +}$ appear at higher uranium concentrations and the hydroxo complexes with the composition 2–3, 2–4, 3–4, 3–5, and 3–6 exist in a range from pH 3 up to that of uranyl hydroxide precipitation.

Fig. 5
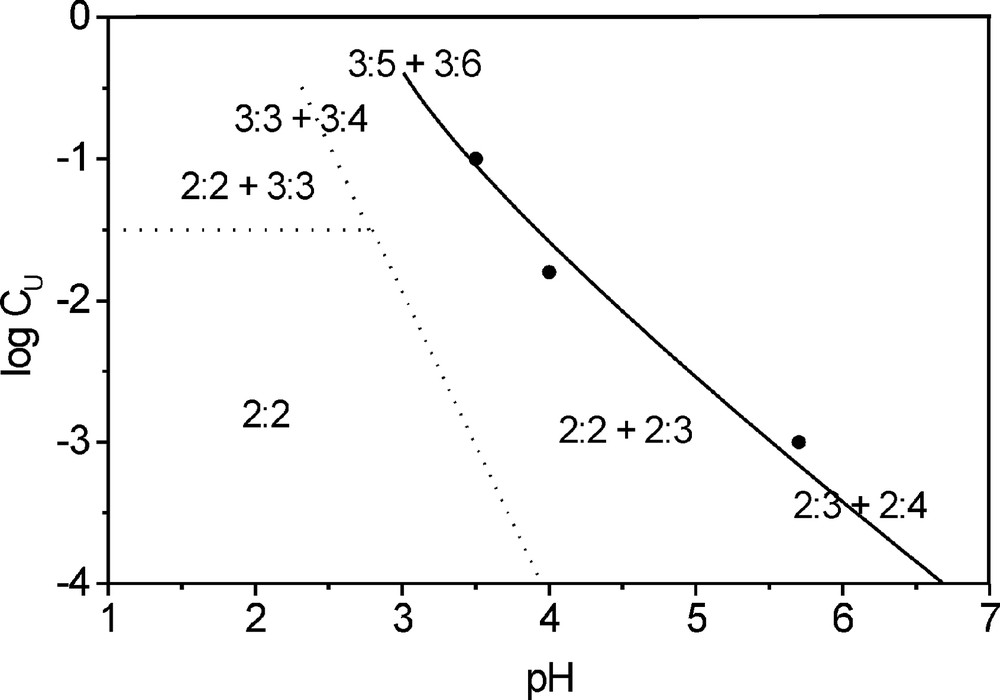
Fields of existence of uranyl hydroxo complexes from the evidence of data about the kinetics of uranyl oxygen exchange.

Our data on uranyl hydrolysis in acidic aqueous solutions are close to Meinrath's data [19]. Based on the analysis of electronic absorption spectra of aqueous uranyl solutions at 550 nm, Meinrath concluded that this spectrum is initiated by a superposition of spectra of three uranyl species. The first one is, by definition, the hydrated uranyl ion. The second was assigned to the 2–2 complex, and the third to the 3–5 complex, based on the published data [7,8]. Taking into account that, in the considered C_U and pH ranges, the concentration of the 3–5 complex is negligible in comparison with those of the other two species, we can conclude that both kinetics of oxygen exchange and electronic absorption spectroscopy give the same conclusion about the existence of the ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ complex only at pH < 3.

The k K₂₂ value calculated from the plots in Fig. 2 for pH 1–3 and C_U 0.003–0.03 M at 25 °C is 2.7 × 10^–8 mol l^–1 s^–1.

4 Conclusion

The uranyl oxygen exchange in acidic aqueous solutions at pH 1–3 suggests the formation of the only ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ dimeric hydroxo complex at uranium concentrations in the range 10^–4–0.03 M. This method suggests that there is no formation of UO₂OH⁺ and (UO₂)₂OH³⁺ complexes, as inferred from the evidence of pH-metry. At uranium concentrations above 0.03 M, the ${({UO}_{2})}_{3} {(OH)}_{3}^{3 +}$ ion and probably larger oligomers can exist. At pH > 3, subsequent hydrolysis of ${({UO}_{2})}_{2} {(OH)}_{2}^{2 +}$ and higher oligomers with formation of ${({UO}_{2})}_{2} {(OH)}_{3}^{+}$ , (UO₂)₂(OH)₄, ${({UO}_{2})}_{3} {(OH)}_{4}^{2 +}$ , etc. complexes is suggested.